Calculate the spring rates for the drag knife, diamond engraver, and collet pen holders by measuring the downforce every 0.5 mm (or so):
Then plotting the data points and eyeballing a straight-line curve fit:
Doing it on hard mode definitely has a certain old-school charm. The graph highlights mis-measured data and similar problems, because, if you don’t see a pretty nearly straight line, something’s gone awry.
But we live in the future, so there’s an easier way:
Well, OK, it’s the future as of the early 1990s, when HP introduced its HP 48 calculators. I’m using the Droid48 emulator on my ancient Google Pixel: living in the past, right here in the future.
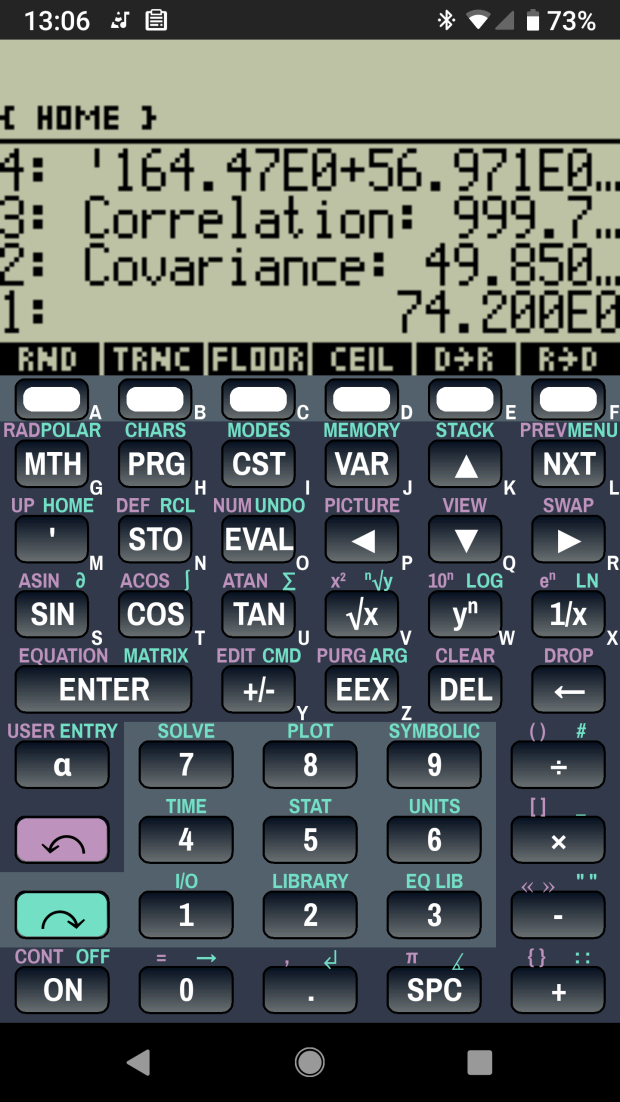
Start by firing up the STAT library (cyan arrow, then the 5 key), selecting Fit Data … from the dropdown list, then selecting the Linear Fit model:
Then tap EDIT and enter the data in a tiny spreadsheet:
My default “engineering mode” numeric display format doesn’t show well on the tiny screen. Tapping the WID→ key helps a bit, but shorter numbers would be better.
With the data entered, set an X value and tap the PRED key to get the corresponding Y value:
Tapping the OK button puts the line’s coefficients on the stack, as shown in the first picture. Write ’em on a strip of tape, stick to the top of the holder, and it’s all good:
Works for me, anyhow.
HP still has the HP 48g manuals online. The (unofficial) HP Museum has a page on the HP 48S. More than you want to know about the 48 series.







MY brain is probably broken and I’m missing something obvious here but what exactly does “zero” mean here? The point at which the pen tip first contacts the bed/work? The zero at which it was touched-off on the length probe (at what force?) Or is it just some arbitrary imaginary point where the fit crosses the axis and means nothing?
If you could precisely touch off a perfectly rigid tool on a hard surface with exactly zero force, then the tip would encounter the preload force when it moved one epsilon more. Back here in the real world, the force rapidly increases from zilch to pretty close to the preload within the first few tenths of a millimeter after contact, while the bearings suck up their stiction / the spring starts bending / the shank settles down to moving.
Cranking another turn on the screws to compress the spring by 0.7 mm (for an M4×0.7 screw) increases the Y-axis intercept by just about 0.7 × the line slope, so the numbers hold together surprisingly well.