The LinuxCNC G2/G3 arc command doc has this to say about numerical precision:
When programming arcs an error due to rounding can result from using a precision of less than 4 decimal places (0.0000) for inch and less than 3 decimal places (0.000) for millimeters.
So I normally set GCMC to produce three decimal digits, because its default of eight digits seems excessive for my usual millimeter measurements, and assume whatever G-Code sender I use won’t chop digits off the end in passing. Mistakenly setting bCNC to round at two decimal places showed what happens with fewer digits, as bCNC’s default is four decimal digits.
A closer look at the coordinates in the lower right part of the spreadsheets (from yesterday) shows the limited accuracy with two decimal digits:
The red blocks mark the first failing arc, where the relative error falls out of tolerance. If GRBL were less fussy (which it should not be), then the next arcs would proceed as shown.
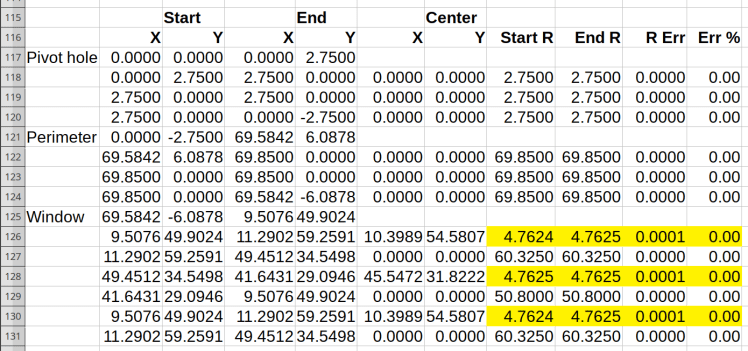
Rounding to three decimal digits pushes the errors into to the third place, with the yellow highlight marking the worst errors:
As you should expect, the smallest arcs have the largest relative errors, although they’re now well within GRBL’s (and LinuxCNC’s, for that matter) limits.
Rounding to four decimal digits makes the errors vanishingly small:
So, by and large, don’t scrimp on the decimal digits … but we knew that already.
I’d been setting GRBL to produce three decimal places, but now I’m using four. Adding a few characters to each G-Code command reduces the number of commands fitting into GRBL’s buffer space, but bCNC normally keeps it around 90% full, so the path planner should remain perfectly happy.
The Smell of Molten Projects in the Morning 