Tag: SDR

Software Defined Radios and circuitry

Crystal Modeling: Parasitic Capacitor Values

A Circuit Cellar reader asked for a better explanation of the parasitic capacitors inside a quartz crystal can than I provided in my April 2017 Circuit Cellar column. Here’s the schematic, with values for a 32 kHz tuning fork resonator and the original caption:

Figure 1 – The mechanical properties of quartz resonators determine the values of the “motional” electrical components in the bottom branch of its circuit model. These values correspond to a 32.768 kHz quartz tuning fork resonator: the 10.4 kH inductor is not a misprint!

I wrote this about the caps:

The value of C0 in the model’s middle branch corresponds to the capacitance between the electrodes plated onto the quartz. The 3.57954 MHz crystal in the title photo, with two silver electrodes deposited on a flat insulating disk, closely resembles an ordinary capacitor. You can measure a crystal’s C0 using a capacitance meter.
However, each of those electrodes also has a capacitance to the resonator’s metal case. The top branch of the model shows two capacitors in series, with Cpar representing half the total parasitic capacitance measured between both leads and the case. Grounding the case, represented by the conductor between the capacitors, by soldering it to the ground plane of an RF circuit eliminates any signal transfer through those capacitors. They will appear as shunt capacitors between the pins and ground; in critical applications, you must add their capacitance to the external load capacitors.

And this about the measurement technique, using a fixture on my AADE LC meter:

With the resonator case captured under the clip on the far right and both its leads held by the clip to the upper left, the meter measures Cpar, the lead-to-case parasitic capacitance. The meter will display twice the value of each parasitic capacitor, at least to a good approximation, because they are in parallel. The five resonators averaged 0.45 pF, with each lead having about 0.25 pF of capacitance to the case. Obviously, measuring half a picofarad requires careful zeroing and a stable fixture: a not-quite-tight banana jack nut caused baffling errors during my first few measurements.
With the resonator repositioned as shown in Photo 2, with one lead under each clip, the meter measures C0, the lead-to-lead capacitance. After careful zeroing, the resonators averaged 0.85 pF.
Although the parasitic lead-to-case capacitors are in parallel with C0, their equivalent capacitance is only Cpar/4 = 0.1 pF. That’s close enough to the measurement error for C0, so I ignored it by rounding C0 upward.

He quite correctly pointed out:

With both leads connected together on one side, then that essentially constitutes a single electrical element inside the case. And with the case being a single element, this configuration in the test fixture seems like a single capacitor with one lead being the case and the other lead being the pins, with a vacuum dielectric.

I would think the meter would display the total capacitance rather than twice the value … It makes sense to me to later say Cpar/2 when the leads are not connected together.

Here’s my second pass at the problem:

… the two-capacitor model comes from the common-case condition, where each lead displays a (nominally equal) parasitic capacitance to the case, because the crystal mounting is reasonably symmetric inside the can. It’s easiest to measure the total capacitance with the leads shorted together, because it’s in the low pF range, then divide by two to get the value of each lead-to-case cap.

[…]

For “real” RF circuits with larger (HC-49 -ish) crystals in parallel-resonance mode, you ground the case and subtract the parasitic capacitance at each lead from the external load capacitors. That’s the usual situation for microprocessor clock oscillators: the crystal sits across the clock amplifier pins, with two more-or-less equal caps from the pins to ground. You should subtract the internal parasitic caps from the clock’s specified load caps, but in practice the values are so small and the cap tolerance so large that it mostly doesn’t matter.

[…]

Un-grounding the case puts those two parasitic caps in series, just as with two discrete caps, so the lead-to-lead capacitance is (or should be!) half of each: 1/4 of the both-leads-to-case value.

Re-reading yet again says I glossed over the effect of having C0 in parallel with the Cpar/2 caps, but methinks dragging those complications into the model benefits only the theoreticians among us (or those working very close to the edge of the possible).

To make it worse, I also botched the QEX reference, which should be Jan/Feb 2016, not 2017. Verily, having a column go read-only makes the errors jump right off the page. [sigh]

At least I can point to this and amend as needed.

2017-07-10

AD9850 Module: Oscillator Thermal Time Constant

With an LM75 atop the 125 MHz oscillator and the whole thing wrapped in foam:

LM75A Temperature Sensor - installed — LM75A Temperature Sensor – installed

Let it cool overnight in the Basement Laboratory, fire it up, record the temperature every 30 seconds, and get the slightly chunky blue curve:

125 MHz Oscillator - Heating Time Constant — 125 MHz Oscillator – Heating Time Constant

Because we know this is one of those exponential-approach problems, the equation looks like:

Temp(t) = T_final + (T_init - T_final) × e^-t/τ

We can find the time constant by either going through the hassle of an RMS curve fit or just winging it by assuming:

The initial temperature, which is 22.5 °C = close to 22.7 °C ambient
The final temperature (call it 42 °C)
Any good data point will suffice

The point at 480 s is a nice, round 40 °C, so plug ’em in:

40.0 = 42.0 + (22.7 - 42.0) × e^-480/τ

Turning the crank produces τ = 212 s, which looks about right.

Trying it again with the 36.125 °C point at 240 s pops out 200.0 °C.

Time for a third opinion!

Because we live in the future, the ever-so-smooth red curve comes from unleashing LibreOffice Calc’s Goal Seek to find a time constant that minimizes the RMS Error. After a moment, it suggests 199.4 s, which I’ll accept as definitive.

The spreadsheet looks like this:

T_init	22.5
T_final	42.0
Tau	199.4

Time s	Temp °C	Exp App	Error²
0	22.250	22.500	0.063
30	25.500	25.224	0.076
60	28.000	27.567	0.187
90	30.125	29.583	0.294
120	31.750	31.317	0.187
150	33.250	32.810	0.194
180	34.375	34.093	0.079
210	35.375	35.198	0.031
240	36.125	36.148	0.001
270	36.813	36.965	0.023
300	37.500	37.668	0.028
330	38.125	38.273	0.022
360	38.500	38.794	0.086
390	39.000	39.242	0.058
420	39.500	39.627	0.016
450	39.750	39.959	0.043
480	40.000	40.244	0.059
510	40.250	40.489	0.057
540	40.500	40.700	0.040
570	40.750	40.882	0.017
600	41.000	41.038	0.001

		RMS Error	0.273

The Exp App column is the exponential equation, assuming the three variables at the top, the Error² column is the squared error between the measurement and the equation, and the RMS Error cell contains the square root of the average of those squared errors.

The Goal Seeker couldn’t push RMS Error to zero and gave up with Tau = 199.4. That’s sensitive to the initial and final temperatures, but close enough to my back of the envelope to remind me not to screw around with extensive calculations when “two minutes” will suffice.

Basically, after five time constants = 1000 s = 15 minutes, the oscillator is stable enough to not worry about.

2017-07-07

AD9850 DDS Module: 125 MHz Oscillator vs. Temperature, Quadratic Edition

I let the DDS cool down overnight, turned it on, and recorded the frequency offset as a function of temperature as it heated up again:

125 MHz Osc Freq Offset vs Temp – Quadratic – 29 – 43 C

The reduced spacing between the points as the temperature increases shows how fast the oscillator heats up. I zero-beat the 10 MHz output, scribbled the temperature, noted the offset, and iterated as fast as I could. The clump of data over on the right end comes from the previous session with essentially stable temperatures.

I only had to throw out two data points to get such a beautiful fit; the gaps should be obvious.

The fit seems fine from room (well, basement) ambient up to hotter than you’d really like to treat the DDS, so using the quadratic equation should allow on-the-fly temperature compensation. Assuming, of course, the equation matches some version of reality close to the one prevailing in the Basement Laboratory, which remains to be seen.

In truth, it probably doesn’t, because the temperature was changing so rapidly the observations all run a bit behind reality. You’d want a temperature-controlled environment around the PCB to let the oscillator stabilize after each increment, then take the measurements. I am so not going to go there.

The original data:

125 MHz Osc Freq Offset vs Temp – 29 – 43 C – data

2017-07-06
AD9850 DDS Module: 125 MHz Oscillator vs. Temperature, Linear Edition

A day of jockeying the AD9850 DDS oscillator shows an interesting relation between the frequency offset and the oscillator temperature:

DDS Oscillator Frequency Offset vs. Temperature – complete

Now, as it turns out, the one lonely little dot off the line happened just after I lit the board up after a tweak, so the oscillator temperature hadn’t stabilized. Tossing it out produces a much nicer fit:

DDS Oscillator Frequency Offset vs. Temperature

Looks like I made it up, doesn’t it?

The first-order coefficient shows the frequency varies by -36 Hz/°C. The actual oscillator frequency decreases with increasing temperature, which means the compensating offset must become more negative to make the oscillator frequency variable match reality. In previous iterations, I’ve gotten this wrong.

For example, at 42.5 °C the oscillator runs at:

125.000000 MHz - 412 Hz = 124.999588 MHz

Dividing that into 2³² = 34.35985169 count/Hz, which is the coefficient converting a desired frequency into the DDS delta phase register value. Then, to get 10.000000 MHz at the DDS output, you multiply:
10×10⁶ × 34.35985169 = 343.598517×10⁶

Stuff that into the DDS and away it goes.

Warmed half a degree to 43.0 °C, the oscillator runs at:

125.000000 MHz - 430 Hz = 124.999570 MHz

That’s 18 Hz lower, so the coefficient becomes 34.35985667, and the corresponding delta phase for a 10 MHz output is 343.598567×10⁶.

Obviously, you need Pretty Good Precision in your arithmetic to get those answers.

After insulating the DDS module to reduce the effect of passing breezes, I thought the oscillator temperature would track the ambient temperature fairly closely, because of the more-or-less constant power dissipation inside the foam blanket. Which turned out to be the case:

DDS Oscillator Temperature vs. Ambient

The little dingle-dangle shows startup conditions, where the oscillator warms up at a constant room temperature. The outlier dot sits 0.125 °C to the right of the lowest pair of points, being really conspicuous, which was another hint it didn’t belong with the rest of the contestants.

So, given the ambient temperature, the oscillator temperature will stabilize at 0.97 × ambient + 20.24, which is close enough to a nice, even 20 °C hotter.

The insulation blanket reduces short-term variations due to breezes, which, given the -36 Hz/°C = 0.29 ppm temperature coefficient, makes good sense; you can watch the DDS output frequency blow in the breeze. It does, however, increase the oscillator temperature enough to drop the frequency by 720 Hz, so you probably shouldn’t use the DDS oscillator without compensating for at least its zero-th order offset at whatever temperature you expect.

Of course, that’s over a teeny-tiny temperature range, where nearly anything would be linear.

The original data:

DDS Oscillator offset vs temperature – 2017-06-24

2017-07-05

LF Crystal Tester: Joystick for Oscillator Offset Adjustment

With the joystick button and LM75 temperature sensor running, this chunk of code lets you nudge the nominal DDS oscillator frequency by 1 Hz every 100 ms:

	// Zero-beat oscillator to 10 MHz GPS-locked reference

	printf("Zero beat DDS oscillator against GPS\n");

	TempFreq.fx_64 = CALFREQ;

	u8x8.clearDisplay();
	byte ln = 0;
	u8x8.drawString(0,ln++,"10 MHz Zero Beat");
	u8x8.drawString(0,ln++,"<- Joystick ->");
	u8x8.drawString(0,ln++," Button = set ");

	int32_t OldOffset = OscOffset;

	while (analogRead(PIN_JOYBUTTTON) > 500) {

	int ai = analogRead(PIN_JOY_Y) – 512; // totally ad-hoc axes
	if (ai < -100) {
	OscOffset += 1;
	}
	else if (ai > 100) {
	OscOffset -= 1;
	}

	if (OscOffset != OldOffset) {
	ln = 4;
	sprintf(Buffer,"Offset %8ld",OscOffset);
	u8x8.drawString(0,ln++,Buffer);

	CalcOscillator(OscOffset); // recalculate constants

	TempCount.fx_64 = MultiplyFixedPt(TempFreq,CtPerHz); // recalculate delta phase count

	WriteDDS(TempCount.fx_32.high); // should be 10 MHz out!

	OldOffset = OscOffset;
	}

	Wire.requestFrom(LM75_ADDR,2);
	Temperature.fx_32.high = Wire.read();
	Temperature.fx_32.low = (uint32_t)Wire.read() << 24;
	PrintFixedPtRounded(Buffer,Temperature,3);
	ln = 7;
	u8x8.drawString(0,ln,"DDS Temp");
	u8x8.drawString(16-strlen(Buffer),ln++,Buffer);

	delay(100);
	}

	printf("Oscillator offset: %ld\n",OscOffset);

view raw gistfile1.txt hosted with ❤ by GitHub

While that’s happening, you compare the DDS output to a reference frequency on an oscilloscope:

The top trace (and scope trigger) is the GPS-locked 10 MHz reference, the lower trace is the AD9850 DDS output (not through the MAX4165 buffer amp, because bandwidth). If the frequencies aren’t identical, the DDS trace will crawl left or right with respect to the reference: leftward if the DDS frequency is too high, rightward if it’s too low. If the DDS frequency is way off, then the waveform may scamper or run, with the distinct possibility of aliasing on digital scopes; you have been warned.

The joystick acts as a bidirectional switch, rather than an analog input, with the loop determining the step increment and timing. The ad-hoc axis orientation lets you (well, me) push the joystick against the waveform crawl, which gradually slows down and stops when the offset value makes the DDS output match the reference.

The OLED displays the current status:

The lurid red glow along the bottom is lens flare from the amber LED showing the relay is turned on. The slightly dimmer characters across the middle of the display show how the refresh interacts with the camera shutter at 1/30 s exposure.

N.B.: Normally, you know the DDS clock oscillator frequency with some accuracy. Dividing that value into 2³² (for the AD9850) gives you the delta-phase count / frequency ratio that converts a desired DDS output frequency into the delta-phase value telling the DDS to make it happen.

In this case, I want the output frequency to be exactly 10.000000 MHz, so I’m adjusting the oscillator frequency (nominal 125 MHz + offset), calculating the corresponding count-to-Hz ratio, multiplying the ratio by 10.000000 MHz, stuffing the ensuing count into the DDS, and eyeballing what happens. When the oscillator frequency variable matches the actual oscillator frequency, then the actual output will 10.000000 MHz and the ratio will be correct.

Got it? Took me a while.

Although the intent is to tune for best frequency match and move on, you (well, I) can use this to accumulate a table of frequency offset vs. temperature pairs, from which a (presumably simple) formula can be conjured to render this step unnecessary.

The Arduino source code as a GitHub Gist:

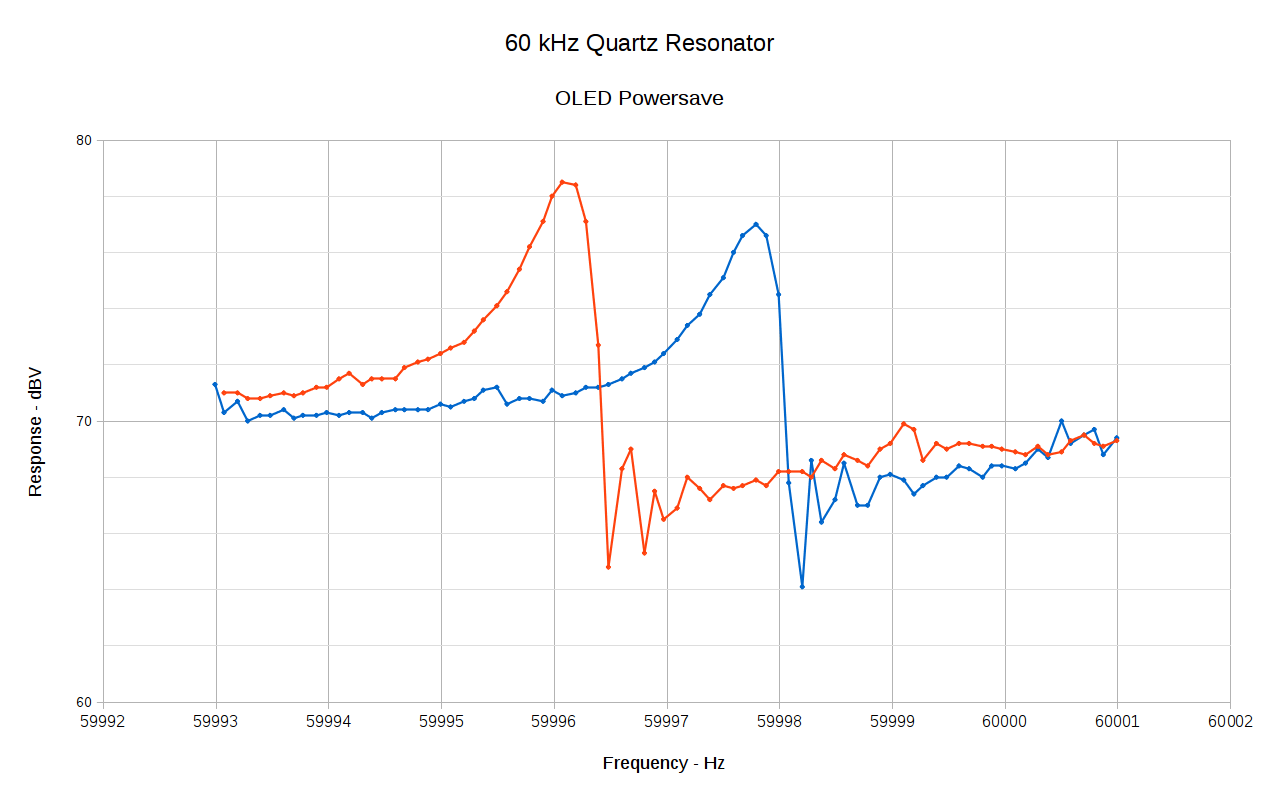
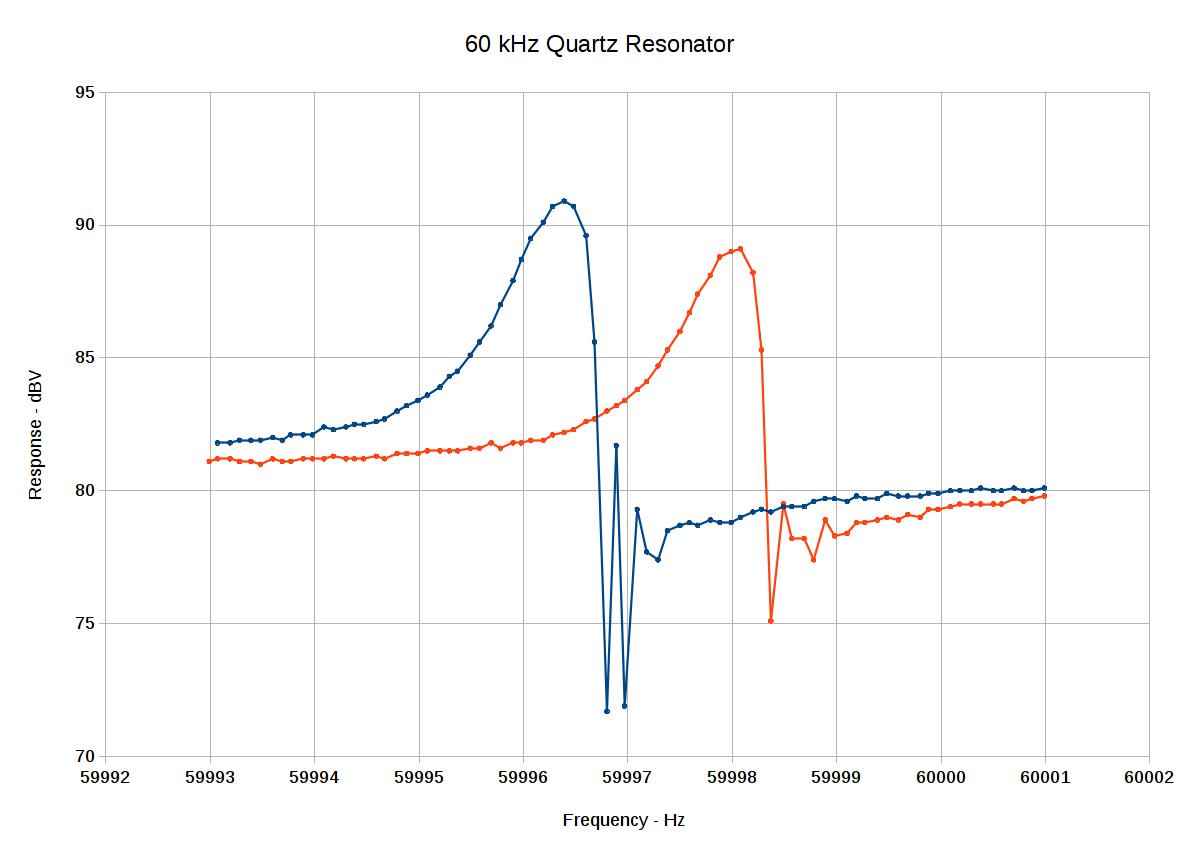
	// 60 kHz crystal tester
	// Ed Nisley – KE4ZNU

	#include <avr/pgmspace.h>
	#include <U8g2lib.h>
	#include <U8x8lib.h>
	#include <Adafruit_MCP4725.h>

	//———————
	// Pin locations

	#define PIN_SYNC 5

	#define PIN_CX_SHORT 6

	#define PIN_DDS_RESET 7
	#define PIN_DDS_LATCH 8

	#define PIN_HEARTBEAT 9

	#define PIN_LOG_AMP A0

	#define PIN_JOYBUTTTON A1
	#define PIN_JOY_Y A2
	#define PIN_JOY_X A3

	// SPI & I2C use hardware support: these pins are predetermined

	#define PIN_SS 10
	#define PIN_MOSI 11
	#define PIN_MISO 12
	#define PIN_SCK 13

	#define PIN_IIC_SDA A4
	#define PIN_IIC_SCL A5

	// IIC Hardware addresses
	// OLED library uses its default address

	#define LM75_ADDR 0x48
	#define SH1106_ADDR 0x70
	#define MCP4725_ADDR 0x60

	// Useful constants

	#define GIGA 1000000000LL
	#define MEGA 1000000LL
	#define KILO 1000LL

	#define ONE_FX (1LL << 32)

	#define CALFREQ (10LL * MEGA * ONE_FX)

	// Structures for 64-bit fixed point numbers
	// Low word = fractional part
	// High word = integer part

	struct ll_fx {
	uint32_t low; // fractional part
	uint32_t high; // integer part
	};

	union ll_u {
	uint64_t fx_64;
	struct ll_fx fx_32;
	};

	// Define semi-constant values

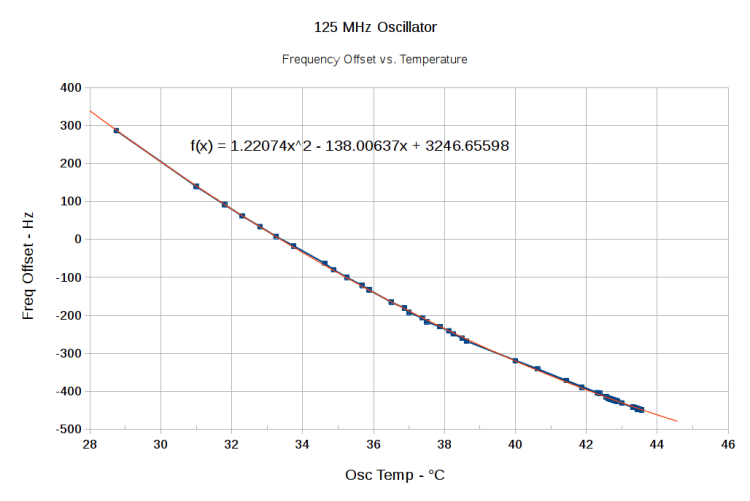
	union ll_u CenterFreq = {(60000 – 4) * ONE_FX}; // center of scan
	//union ll_u CenterFreq = {(32768 – 2) * ONE_FX}; // center of scan

	#define NOMINAL_OSC ((125 * MEGA) * ONE_FX)
	union ll_u Oscillator = {NOMINAL_OSC}; // oscillator frequency
	int32_t OscOffset = -414; // measured offset from NOMINAL_OSC

	uint16_t ScanWidth = 4*2; // width must be an even integer
	uint16_t ScanSettleMS = 2000; // milliseconds of settling time per measurement

	union ll_u ScanStepSize = {ONE_FX / 10}; // 0.1 Hz is smallest practical decimal step
	//union ll_u ScanStepSize = {ONE_FX / 34}; // 0.0291 is smallest possible step

	// Global variables of interest to everyone

	union ll_u ScanFrom, ScanTo; // may be larger than unsigned ints
	union ll_u ScanFreq; // fixed-point frequency scan settings

	union ll_u PeakFreq; // records maximum response point
	union ll_u PeakdB; // and corresponding log amp output

	union ll_u SeriesPeakLow,SeriesPeakHigh; // peak with CX short and CX in circuit

	union ll_u CtPerHz; // will be 2^32 / oscillator
	union ll_u HzPerCt; // will be oscillator / 2^32

	char Buffer[10+1+10+1]; // string buffer for fixed point number conversions

	union ll_u Temperature; // read from LM75A

	// Hardware library variables

	U8X8_SH1106_128X64_NONAME_HW_I2C u8x8(U8X8_PIN_NONE);
	//U8X8_SH1106_128X64_NONAME_4W_HW_SPI u8x8(PIN_DISP_SEL, PIN_DISP_DC , PIN_DISP_RST);
	//U8X8_SH1106_128X64_NONAME_4W_SW_SPI u8x8(PIN_SCK, PIN_MOSI, PIN_DISP_SEL, PIN_DISP_DC , PIN_DISP_RST);

	#define DAC_WR false
	#define DAC_WR_EEP true
	#define DAC_BITS 12
	#define DAC_MAX 0x0fff

	Adafruit_MCP4725 XAxisDAC; // I²C DAC for X axis output
	uint32_t XAxisValue; // DAC parameter uses 32 bits

	union ll_u LogAmpdB; // computed dB value

	#define HEARTBEAT_MS 3000

	unsigned long MillisNow,MillisThen;

	//———–
	// Useful functions

	// Pin twiddling

	void TogglePin(char bitpin) {
	digitalWrite(bitpin,!digitalRead(bitpin)); // toggle the bit based on previous output
	}

	void PulsePin(char bitpin) {
	TogglePin(bitpin);
	TogglePin(bitpin);
	}

	void WaitButtonDown() {
	word ai;

	do {
	ai = analogRead(PIN_JOYBUTTTON);
	} while (ai > 500);
	}

	void WaitButtonUp() {
	word ai;

	do {
	ai = analogRead(PIN_JOYBUTTTON);
	} while (ai < 500);
	}

	// Hardware-assisted SPI I/O

	void EnableSPI(void) {
	digitalWrite(PIN_SS,HIGH); // set SPI into Master mode
	SPCR \|= 1 << SPE;
	}

	void DisableSPI(void) {
	SPCR &= ~(1 << SPE);
	}

	void WaitSPIF(void) {
	while (! (SPSR & (1 << SPIF))) {
	// TogglePin(PIN_HEARTBEAT);
	// TogglePin(PIN_HEARTBEAT);
	continue;
	}
	}

	byte SendRecSPI(byte Dbyte) { // send one byte, get another in exchange
	SPDR = Dbyte;
	WaitSPIF();

	return SPDR; // SPIF will be cleared
	}

	//————–
	// DDS module

	void EnableDDS(void) {

	digitalWrite(PIN_DDS_LATCH,LOW); // ensure proper startup

	digitalWrite(PIN_DDS_RESET,HIGH); // minimum reset pulse 40 ns, not a problem
	digitalWrite(PIN_DDS_RESET,LOW);
	delayMicroseconds(1); // max latency 100 ns, not a problem

	DisableSPI(); // allow manual control of outputs
	digitalWrite(PIN_SCK,LOW); // ensure clean SCK pulse
	PulsePin(PIN_SCK); // … to latch hardwired config bits
	PulsePin(PIN_DDS_LATCH); // load hardwired config bits = begin serial mode

	EnableSPI(); // turn on hardware SPI controls
	SendRecSPI(0x00); // shift in serial config bits
	PulsePin(PIN_DDS_LATCH); // load serial config bits

	}

	// Write delta phase count to DDS
	// This comes from the integer part of a 64-bit scaled value

	void WriteDDS(uint32_t DeltaPhase) {

	SendRecSPI((byte)DeltaPhase); // low-order byte first
	SendRecSPI((byte)(DeltaPhase >> 8));
	SendRecSPI((byte)(DeltaPhase >> 16));
	SendRecSPI((byte)(DeltaPhase >> 24));

	SendRecSPI(0x00); // 5 MSBs = phase = 0, 3 LSBs must be zero

	PulsePin(PIN_DDS_LATCH); // write data to DDS
	}

	//————–
	// Log amp module

	#define LOG_AMP_SAMPLES 10
	#define LOG_AMP_DELAYMS 10

	uint64_t ReadLogAmp() {

	union ll_u LogAmpRaw;

	LogAmpRaw.fx_64 = 0;
	for (byte i=0; i<LOG_AMP_SAMPLES; i++) {
	LogAmpRaw.fx_32.high += analogRead(PIN_LOG_AMP);
	delay(LOG_AMP_DELAYMS);
	}

	LogAmpRaw.fx_64 /= LOG_AMP_SAMPLES; // figure average from totally ad-hoc number of samples

	LogAmpRaw.fx_64 *= 5; // convert from ADC counts to voltage
	LogAmpRaw.fx_64 /= 1024;

	LogAmpRaw.fx_64 /= 24; // convert from voltage to dBV at 24 mV/dBV
	LogAmpRaw.fx_64 *= 1000;

	return LogAmpRaw.fx_64;
	}

	//———–
	// Scan DDS and record response

	void ScanCrystal() {

	byte ln;
	union ll_u Temp, TestFreq, TestCount;

	XAxisValue = 0;
	PeakdB.fx_64 = 0;

	printf("CX: %s\n",digitalRead(PIN_CX_SHORT) ? "short" : "enable");

	for (ScanFreq = ScanFrom;
	ScanFreq.fx_64 < (ScanTo.fx_64 + ScanStepSize.fx_64 / 2);
	ScanFreq.fx_64 += ScanStepSize.fx_64) {

	digitalWrite(PIN_SYNC,HIGH);

	TestCount.fx_64 = MultiplyFixedPt(ScanFreq,CtPerHz); // compute DDS delta phase
	TestCount.fx_32.low = 0; // truncate count to integer
	TestFreq.fx_64 = MultiplyFixedPt(TestCount,HzPerCt); // compute actual frequency

	Temp.fx_64 = (DAC_MAX * (ScanFreq.fx_64 – ScanFrom.fx_64)); // figure X as fraction
	Temp.fx_64 /= ScanWidth;
	XAxisValue = Temp.fx_32.high;

	digitalWrite(PIN_HEARTBEAT,HIGH);
	WriteDDS(TestCount.fx_32.high); // set DDS to new frequency
	XAxisDAC.setVoltage(XAxisValue,DAC_WR); // and set X axis to match
	digitalWrite(PIN_SYNC,LOW);

	if (ScanFreq.fx_64 == ScanFrom.fx_64) {
	delay(3*ScanSettleMS); // very long settling time
	}
	else {
	delay(ScanSettleMS); // small steps are faster
	}

	LogAmpdB.fx_64 = ReadLogAmp(); // fetch avg value

	if (LogAmpdB.fx_64 > PeakdB.fx_64) { // hit a new high?
	PeakFreq = TestFreq; // save actual frequency
	PeakdB = LogAmpdB;

	ln = digitalRead(PIN_CX_SHORT) ? 4 : 5; // CX selects row
	PrintFixedPtRounded(Buffer,TestFreq,2); // display actual peak
	u8x8.drawString(0,ln,Buffer);

	PrintFixedPtRounded(Buffer,LogAmpdB,1); // tack on response
	u8x8.drawString(16-strlen(Buffer),ln,Buffer);
	}

	ln = 0;
	PrintFixedPtRounded(Buffer,TestFreq,2); // display current frequency
	u8x8.draw2x2String(0,ln++,Buffer);
	ln++; // double-high characters
	printf("%9s ",Buffer); // log to serial port

	PrintFixedPtRounded(Buffer,LogAmpdB,1); // display response
	u8x8.drawString(0,ln,"dBV ");
	u8x8.drawString(16-strlen(Buffer),ln++,Buffer);
	printf(", %6s\n",Buffer); // and log it

	}

	}

	//———–
	// Round scaled fixed point to specific number of decimal places: 0 through 8
	// You should display the value with only Decimals characters beyond the point
	// Must calculate rounding value as separate variable to avoid mystery error

	uint64_t RoundFixedPt(union ll_u TheNumber,unsigned Decimals) {
	union ll_u Rnd;

	Rnd.fx_64 = (ONE_FX >> 1) / (pow(10LL,Decimals)); // that's 0.5 / number of places
	TheNumber.fx_64 = TheNumber.fx_64 + Rnd.fx_64;

	return TheNumber.fx_64;
	}


	//———–
	// Multiply two unsigned scaled fixed point numbers without overflowing a 64 bit value
	// Perforce, the product of the two integer parts mut be < 2^32

	uint64_t MultiplyFixedPt(union ll_u Mcand, union ll_u Mplier) {
	union ll_u Result;

	Result.fx_64 = ((uint64_t)Mcand.fx_32.high * (uint64_t)Mplier.fx_32.high) << 32; // integer parts (clear fract)
	Result.fx_64 += ((uint64_t)Mcand.fx_32.low * (uint64_t)Mplier.fx_32.low) >> 32; // fraction parts (always < 1)
	Result.fx_64 += (uint64_t)Mcand.fx_32.high * (uint64_t)Mplier.fx_32.low; // cross products
	Result.fx_64 += (uint64_t)Mcand.fx_32.low * (uint64_t)Mplier.fx_32.high;

	return Result.fx_64;
	}


	//———–
	// Long long print-to-buffer helpers
	// Assumes little-Endian layout

	void PrintHexLL(char *pBuffer,union ll_u FixedPt) {
	sprintf(pBuffer,"%08lx %08lx",FixedPt.fx_32.high,FixedPt.fx_32.low);
	}

	// converts all 9 decimal digits of fraction, which should suffice

	void PrintFractionLL(char *pBuffer,union ll_u FixedPt) {
	union ll_u Fraction;

	Fraction.fx_64 = FixedPt.fx_32.low; // copy 32 fraction bits, high order = 0
	Fraction.fx_64 *= GIGA; // times 10^9 for conversion
	Fraction.fx_64 >>= 32; // align integer part in low long
	sprintf(pBuffer,"%09lu",Fraction.fx_32.low); // convert low long to decimal
	}

	void PrintIntegerLL(char *pBuffer,union ll_u FixedPt) {
	sprintf(pBuffer,"%lu",FixedPt.fx_32.high);
	}

	void PrintFixedPt(char *pBuffer,union ll_u FixedPt) {
	PrintIntegerLL(pBuffer,FixedPt); // do the integer part
	pBuffer += strlen(pBuffer); // aim pointer beyond integer
	*pBuffer++ = '.'; // drop in the decimal point, tick pointer
	PrintFractionLL(pBuffer,FixedPt);
	}

	void PrintFixedPtRounded(char *pBuffer,union ll_u FixedPt,unsigned Decimals) {
	char *pDecPt;

	FixedPt.fx_64 = RoundFixedPt(FixedPt,Decimals);

	PrintIntegerLL(pBuffer,FixedPt); // do the integer part
	pBuffer += strlen(pBuffer); // aim pointer beyond integer

	pDecPt = pBuffer; // save the point location
	*pBuffer++ = '.'; // drop in the decimal point, tick pointer

	PrintFractionLL(pBuffer,FixedPt); // do the fraction

	if (Decimals == 0)
	*pDecPt = 0; // 0 places means discard the decimal point
	else
	*(pDecPt + Decimals + 1) = 0; // truncate string to leave . and Decimals chars

	}

	//———–
	// Calculate useful "constants" from oscillator info
	// Offset is integer Hz, because 0.1 ppm = 1 Hz at 10 MHz is as close as we can measure

	void CalcOscillator(int32_t Offset) {

	Oscillator.fx_64 = NOMINAL_OSC + ((int64_t)Offset << 32);

	HzPerCt.fx_32.low = Oscillator.fx_32.high; // divide oscillator by 2^32 with simple shifting
	HzPerCt.fx_32.high = 0;

	CtPerHz.fx_64 = -1; // Compute (2^32 – 1) / oscillator
	CtPerHz.fx_64 /= (uint64_t)Oscillator.fx_32.high; // remove 2^32 scale factor from divisor

	}

	//– Helper routine for printf()

	int s_putc(char c, FILE *t) {
	Serial.write(c);
	}

	//———–

	void setup () {

	union ll_u TempFreq,TempCount;

	pinMode(PIN_HEARTBEAT,OUTPUT);
	digitalWrite(PIN_HEARTBEAT,LOW); // show we got here

	pinMode(PIN_SYNC,OUTPUT);
	digitalWrite(PIN_SYNC,LOW);

	Serial.begin (115200);
	fdevopen(&s_putc,0); // set up serial output for printf()

	Serial.println (F("60 kHz Crystal Tester"));
	Serial.println (F("Ed Nisley – KE4ZNU – June 2017\n"));

	// DDS module controls

	pinMode(PIN_DDS_LATCH,OUTPUT);
	digitalWrite(PIN_DDS_LATCH,LOW);
	pinMode(PIN_DDS_RESET,OUTPUT);
	digitalWrite(PIN_DDS_RESET,HIGH);

	// Light up the display

	Serial.println("Initialize OLED");
	u8x8.begin();
	u8x8.setFont(u8x8_font_artossans8_r);
	// u8x8.setPowerSave(0);

	u8x8.setFont(u8x8_font_pxplusibmcga_f);
	u8x8.draw2x2String(0,0,"XtalTest");
	u8x8.drawString(0,3,"Ed Nisley");
	u8x8.drawString(0,4," KE4ZNU");
	u8x8.drawString(0,6,"June 2017");

	// configure SPI hardware

	pinMode(PIN_SS,OUTPUT); // set up manual controls
	digitalWrite(PIN_SS,HIGH);
	pinMode(PIN_SCK,OUTPUT);
	digitalWrite(PIN_SCK,LOW);
	pinMode(PIN_MOSI,OUTPUT);
	digitalWrite(PIN_MOSI,LOW);

	pinMode(PIN_MISO,INPUT_PULLUP);

	SPCR = B00110000; // Auto SPI: no int, disabled, LSB first, master, + edge, leading, f/4
	SPSR = B00000000; // not double data rate

	TogglePin(PIN_HEARTBEAT); // show we got here

	// Set up X axis DAC output

	XAxisDAC.begin(MCP4725_ADDR); // start up MCP4725 DAC at Sparkfun address
	// XAxisDAC.setVoltage(0,DAC_WR_EEP); // do this once per DAC to set power-on at 0 V
	XAxisDAC.setVoltage(0,DAC_WR); // force 0 V after a reset without a power cycle

	// LM75A temperature sensor requires no setup!

	// External capacitor in test fixture

	pinMode(PIN_CX_SHORT,OUTPUT);
	digitalWrite(PIN_CX_SHORT,HIGH); // short = remove external cap

	// Scan limits and suchlike

	ScanFrom.fx_64 = CenterFreq.fx_64 – (ONE_FX * ScanWidth/2);
	ScanTo.fx_64 = CenterFreq.fx_64 + (ONE_FX * ScanWidth/2);

	PrintFixedPtRounded(Buffer,CenterFreq,1);
	printf("Center freq: %s Hz\n",Buffer);
	printf("Settling time: %d ms\n",ScanSettleMS);

	// Wake up and load the DDS

	CalcOscillator(OscOffset); // use default oscillator frequency

	Serial.print("\nStarting DDS: ");
	TempFreq.fx_64 = CALFREQ;
	TempCount.fx_64 = MultiplyFixedPt(TempFreq,CtPerHz);
	// PrintHexLL(Buffer,TempCount);
	// printf(" Count: %s ",Buffer);

	EnableDDS();

	WriteDDS(TempCount.fx_32.high);
	Serial.println("running\n");

	// Zero-beat oscillator to 10 MHz GPS-locked reference

	printf("Zero beat DDS oscillator against GPS\n");

	TempFreq.fx_64 = CALFREQ;

	u8x8.clearDisplay();
	byte ln = 0;
	u8x8.drawString(0,ln++,"10 MHz Zero Beat");
	u8x8.drawString(0,ln++,"<- Joystick ->");
	u8x8.drawString(0,ln++," Button = set ");

	int32_t OldOffset = OscOffset;

	while (analogRead(PIN_JOYBUTTTON) > 500) {

	int ai = analogRead(PIN_JOY_Y) – 512; // totally ad-hoc axes
	if (ai < -100) {
	OscOffset += 1;
	}
	else if (ai > 100) {
	OscOffset -= 1;
	}

	if (OscOffset != OldOffset) {
	ln = 4;
	sprintf(Buffer,"Offset %8ld",OscOffset);
	u8x8.drawString(0,ln++,Buffer);

	CalcOscillator(OscOffset); // recalculate constants

	TempCount.fx_64 = MultiplyFixedPt(TempFreq,CtPerHz); // recalculate delta phase count

	WriteDDS(TempCount.fx_32.high); // should be 10 MHz out!

	OldOffset = OscOffset;
	}

	Wire.requestFrom(LM75_ADDR,2);
	Temperature.fx_32.high = Wire.read();
	Temperature.fx_32.low = (uint32_t)Wire.read() << 24;
	PrintFixedPtRounded(Buffer,Temperature,3);
	ln = 7;
	u8x8.drawString(0,ln,"DDS Temp");
	u8x8.drawString(16-strlen(Buffer),ln++,Buffer);

	delay(100);
	}

	printf("Oscillator offset: %ld\n",OscOffset);

	u8x8.clearDisplay();

	Serial.println("\nStartup done\n");

	MillisThen = millis();
	}

	//———–

	void loop () {

	byte ln;
	union ll_u Temp;

	u8x8.setPowerSave(0);
	u8x8.clearDisplay();
	ln = 0;
	u8x8.draw2x2String(0,2*ln++,"Press");
	u8x8.draw2x2String(0,2*ln++,"Button");
	u8x8.draw2x2String(0,2*ln++,"To Start");
	u8x8.draw2x2String(0,2*ln++,"Test");
	printf("Waiting for button press: ");

	WaitButtonDown();

	printf("\n");

	u8x8.clearDisplay();
	// u8x8.setPowerSave(1);

	// Report temperature

	Wire.requestFrom(LM75_ADDR,2);
	Temperature.fx_32.high = Wire.read();
	Temperature.fx_32.low = (uint32_t)Wire.read() << 24;
	PrintFixedPtRounded(Buffer,Temperature,3);
	printf("Oscillator temperature: %s C\n",Buffer);
	ln = 3;
	u8x8.drawString(0,ln,"DDS Temp");
	u8x8.drawString(16-strlen(Buffer),ln,Buffer);

	// First scan: CX shorted

	digitalWrite(PIN_CX_SHORT,HIGH);
	delay(10);

	ScanCrystal();

	SeriesPeakLow = PeakFreq;

	PrintFixedPtRounded(Buffer,PeakFreq,2); // report peak freq
	printf("\nPeak: %s Hz",Buffer);

	PrintFixedPtRounded(Buffer,PeakdB,1); // tack on response
	printf(" %s dbV\n",Buffer);

	// Second scan: CX in circuit

	digitalWrite(PIN_CX_SHORT,LOW);
	delay(10);

	ScanFrom.fx_64 = SeriesPeakLow.fx_64 – (2 * ONE_FX); // tighten scan limits
	ScanFrom.fx_32.low = 0;
	ScanTo.fx_64 = SeriesPeakLow.fx_64 + (4 * ONE_FX);
	ScanTo.fx_32.low = 0;

	ScanCrystal();

	SeriesPeakHigh = PeakFreq;

	PrintFixedPtRounded(Buffer,PeakFreq,2); // report peak freq
	printf("\nPeak: %s Hz",Buffer);

	PrintFixedPtRounded(Buffer,PeakdB,1); // tack on response
	printf(" %s dbV\n",Buffer);

	ln = 0;
	u8x8.draw2x2String(0,ln," -Done- ");
	ln +=2;
	u8x8.clearLine(ln);

	ln = 6;
	Temp.fx_64 = SeriesPeakHigh.fx_64 – SeriesPeakLow.fx_64;
	PrintFixedPtRounded(Buffer,Temp,2);
	printf("Delta frequency: %s\n",Buffer);
	u8x8.drawString(0,ln,"Delta freq");
	u8x8.drawString(16-strlen(Buffer),ln,Buffer);

	ln = 7;
	u8x8.drawString(0,ln,"Press button …");

	u8x8.setPowerSave(0);

	WaitButtonDown();

	WaitButtonUp();


	}

view raw CrystalTester.ino hosted with ❤ by GitHub

2017-07-03

LF Crystal Tester: Bring the Noise!

The OLED display refresh contributes 100 Hz noise pulses to the low-level sine wave from the crystal test fixture:

OLED Enabled – 100 Hz display refresh

Disabling the display by activating its powersave option reveals 60 Hz pulses from the USB port on the Arduino Nano:

OLED Powersave – 60 Hz USB Ground Loop

Unplugging the USB cable, leaving just the +5 VDC power supply and coax cable to the oscilloscope, solves most of the problem:

OLED Powersave – USB unplugged

A closer look shows some (relatively) low frequency noise remains in full effect:

OLED Powersave – USB unplugged – detail

Disabling the display while measuring the crystal seems sensible, although, to avoid surprises, a pushbutton should start the process. Unplugging the USB port puts a real crimp in the data collection, although that’s probably survivable with a USB isolator, one of which is on the way around the planet.

The remaining low-level chop requires more thought. Somewhat to my surprise, holding the Arduino Reset button down doesn’t change much of anything, so it’s not a firmware thing.

Those 10 µF coupling caps gotta go.

With the OLED dark and the USB carrying data:

Spectrum – OLED Powersave – USB in

Compare that to the first pass:

Spectrum-60

Tamping down the noise seems to reduce the overall amplitude variation, but it also makes the capacitor-in and capacitor-out curves more consistent. There may be other things going on that I haven’t accounted for.

The peak frequencies differ by 0.2 Hz, which is probably due to a few degrees of temperature difference. Obviously, it’s badly in need of a temperature calibration & correction.

2017-06-23
LF Crystal Tester: LM75 Temperature Sensor
A strip of NXP (née Philips plus Freescale, including the part of Motorola that didn’t become ON) LM75A I²C temperature sensors arrived from beyond the horizon. To see if they worked, I soldered thin wires directly to the SO-8 pins, entombed it in Kapton tape to prevent spitzensparken, and jammed it under the foam insulation atop the AD9850 DDS module:

AD9850 DDS module with LM75A Temperature Sensor

This turns out to be easier than screwing around with thermistors, because the chip reports the temperature directly in Celcius with ⅛ °C resolution. Classic LM75 chips from National (now absorbed by TI) had ½ °C resolution, but the datasheet shows the bits have an easily extensible format:

LM75A Temperature Data Format

Huh. Fixed-point data, split neatly on a byte boundary. Who’d’a thunk it?

There’s a standard Arduino library using, naturally enough, floating point numbers, but I already have big fixed point numbers lying around and, with the I²C hardware up & running from the X axis DAC and OLED display, this was straightforward:
```
Wire.requestFrom(LM75_ADDR,2);
Temp.fx_32.high = Wire.read();
Temp.fx_32.low = (uint32_t)Wire.read() << 24;
PrintFixedPtRounded(Buffer,Temp,3);
u8x8.drawString(0,ln,"DDS C          ");
u8x8.drawString(16-strlen(Buffer),ln,Buffer);
printf(",%s",Buffer);
ln += 1;
```
The next-to-last line squirts the temperature through the serial port to make those nice plots.

Casually ignoring all I²C bus error conditions will eventually lead to heartache and confusion. In particular, the Basement Laboratory temperature must never fall below 0 °C, because I just plunk the two’s-complement temperature data into an unsigned fixed point number.

Which produces the next-to-bottom line:

DDS OLED with LM75 temperature

Alas, the u8x8 font doesn’t include a degree symbol.

Given sufficient motivation, I can now calibrate the DDS output against the GPS-locked 10 MHz standard to get a (most likely) linear equation for the oscillator frequency offset as a function of temperature. The DDS module includes a comparator to square up its sine wave, so an XOR phase detector or something based on filtering the output of an analog switch might be feasible.
2017-06-22