Improvements – Page 89 – The Smell of Molten Projects in the Morning

Homage Tektronix Circuit Computer: Paper Matters

To judge from the dislodged pigment grains, the original Tektronix Circuit Computer probably used then-new laser printing on good-quality paper, laminated between plastic sheets:

A Pilot Precise V5RT cartridge on plain paper (20 lb 98 white), also laminated, looks pretty good:

Tek CC - V5RT green - 20 lb plain paper — Tek CC – V5RT green – 20 lb plain paper

But a black V5RT pen on HP Glossy Presentation Paper (44 lb, 160 g/m²), also laminated, is spectacular:

Tek CC - V5RT black - glossy presentation paper — Tek CC – V5RT black – glossy presentation paper

The glossy Presentation paper is hard enough to keep the pen ball from sinking in, producing much finer lines. In round numbers:

0.2 mm – Tek laser-printed (?) original
0.3 mm – green V5RT on plain paper
0.2 mm – black V5RT on glossy Presentation paper

The CNC 3018XL plotted / drew everything at 2400 mm/min = 40 mm/s, with minimal wobbulation in the lines and none worth mentioning in the characters.

The pen ball sometimes pulls a dot of ink off the glossy paper as it rises at the end of a stroke; perhaps matte paper would produce more traction on the ink.

You can see small blobs at the end of some strokes, but the fancy paper prevents most of the bleeding visible in the previous tests. Pilot V5 pens definitely dislike card stock.

The results looks great in person without magnification, so maybe none of that matters.

The pix come from the Pixel 3a camera in its microscope adapter.

2019-12-27

Kenmore 158 Sewing Machine: Glare Reduction

The additional LEDs around the needle on (one of) Mary’s Kenmore Model 158 sewing machines provide plenty of light for normal sewing, but produced too much glare on the polished steel “hand hole cover plate” (their nomenclature) for small-scale work. A matte surface seemed in order, which came from some translucent mailing labels left over from our Christmas card effort:

Kenmore 158 - non-glare cover plate — Kenmore 158 – non-glare cover plate

Mailing labels probably aren’t a permanent solution, but they certainly solved the problem without delay. We’re loathe to etch the steel, as increasing the surface roughness definitely isn’t what you want, nor blacken it, for obvious reasons.

Too much light is definitely better than too little, though.

2019-12-26

Merry Christmas

Moonrise, as seen through the pines in our yard:

Pixel 3a Night Vision - moonrise — Pixel 3a Night Vision – moonrise

The Pixel 3a produces exceedingly useful low-light images, mostly by having Google’s software compensate for its tiny lens and minimal light-capture area, with the downside of turning a peaceful night scene into harsh daylight.

Take the rest of the day off, OK?

2019-12-25

Google Pixel 3a Microscope Adapter

Hand-holding my Google Pixel 3a phone over the microscope eyepiece worked well enough to justify building Yet Another Camera Adapter:

Pixel 3a Microscope Adapter - in action — Pixel 3a Microscope Adapter – in action

The solid model looks about like you’d expect:

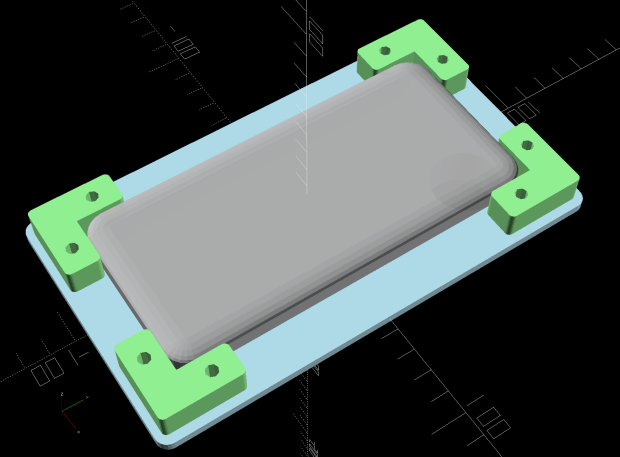
Google Pixel 3a Zoom Microscope Mount - solid model - top — Google Pixel 3a Zoom Microscope Mount – solid model – top

The “camera” actually has the outside dimensions of a Spigen case, rather than the bare phone, because dropping a bare phone is never a good idea.

The base plate pretty much fills the M2’s platform:

Pixel 3a Microscope Adapter - M2 platform — Pixel 3a Microscope Adapter – M2 platform

I originally arranged the four corners around the plate to print everything in one go, but an estimated six hours of print time suggested doing the corners separately would maximize local happiness. Which it did, whew, even if the plate ran for a bit over 4-1/2 hours.

The snout is a loose fit around the 5× widefield microscope eyepiece, with the difference made up in a wrap of black tape; it’s much easier to adjust the fit upward than to bore out the snout. An overwrap of tape secures the snout to the eyepiece, which I’ve dedicated to the cause; the scope normally rocks 10× widefield glass.

The tapered hole exposes the phone’s fingerprint reader to simplify unlocking, should it shut down while I’m fiddling with something else.

The microscope doesn’t fully illuminate the camera’s entrance pupil at minimum zoom, with 4.5× filling the screen and (mostly) eliminating the vignette. The corner blocks have oversize holes to allow aligning the camera lens axis over the microscope optical axis. The solid model incorporates Lessons Learned from the version you see here, because you (well, I) can’t measure the camera axis with respect to the outside dimensions accurately enough:

Pixel 3a Microscope Adapter - installed - front — Pixel 3a Microscope Adapter – installed – front

Although it’s less unsteady than it looks, microscopy requires a gentle touch at the best of times. The adapter doesn’t add much wobble to the outcome:

Pixel 3a Microscope Adapter - installed - side — Pixel 3a Microscope Adapter – installed – side

The field is about 14×19 mm with the camera at 4.5× and the microscope at minimum zoom:

Pixel 3a Microscope Adapter - test image - min mag — Pixel 3a Microscope Adapter – test image – min mag

You can see a little darkening on the upper and lower right corners, so the phone’s still minutely leftward.

The field is about 1.5×2 mm at full throttle:

Pixel 3a Microscope Adapter - test image - max mag — Pixel 3a Microscope Adapter – test image – max mag

Color balance with the cold white LED ring isn’t the best, but it’s survivable. Mad props to OpenCamera for exposing All. The. Controls. you might possibly need.

The OpenSCAD source code as a GitHub Gist:

	// Google Pixel 3a mount for stereo zoom microscope
	// Ed Nisley – KE4ZNU – 2019-12

	Layout = "Show"; // [Show,BuildAll,BuildBumpers,BuildPlate,DrillGuide,Phone,Plate,Bumper]

	/* [Hidden] */

	ThreadThick = 0.25;
	ThreadWidth = 0.40;

	HoleWindage = 0.2;

	Protrusion = 0.1; // make holes end cleanly

	function IntegerMultiple(Size,Unit) = Unit * ceil(Size / Unit);

	ID = 0;
	OD = 1;
	LENGTH = 2;

	inch = 25.4;

	//———————-
	// Dimensions

	Phone = [74.5,156.0,12.0]; // inside Spigen case
	PhoneRadii = [10.0,10.0,3.0]; // corner rounding, likewise

	LensOffset = [-17.0,-18.5,0]; // looking at phone screen, (-) sign = from right/top edge

	PrintReader = [0,Phone.y/2 – 44.0,0]; // fingerprint reader from center
	PrintReaderDia = [20.0,30.0,0]; // … hole for access

	Eyepiece = [11.5,28.0 + 0.50,27.0]; // ID = lens, OD includes clearance

	Insert = [3.0,4.5,4.0]; // M3 threaded brass insert
	Screw = [3.0,7.0,3.5]; // OD = washer, LENGTH = washer + head height

	WallThick = 3.0; // minimum wall thickness

	Bumper = [2*Screw[OD],20.0,Phone.z]; // bumper edge piece
	BumperOAL = Bumper.y + Bumper.x; // outside length for corner piece

	BumperRadius = 2.0;

	MinMargin = 1.2*Bumper.x; // at least this much extra plate for bumpers
	echo(str("MinMargin: ",MinMargin));

	Plate = [IntegerMultiple(Phone.x + 2*MinMargin,5.0),
	IntegerMultiple(Phone.y + 2*MinMargin,5.0),
	false ? 3ThreadThick : max(Insert[LENGTH] + 2ThreadThick,WallThick)];
	PlateRadius = 5.0;
	echo(str("Plate: ",Plate," radius: ",PlateRadius));

	EmbossDepth = 2*ThreadThick + Protrusion;
	DebossHeight = EmbossDepth;

	ScrewOffset = Bumper.x/2;
	ScrewAdjust = 1.5*Screw[ID];

	NumSides = 234;

	Gap = 2.0; // between build layout parts

	//———————-
	// Useful routines

	module PolyCyl(Dia,Height,ForceSides=0) { // based on nophead's polyholes

	Sides = (ForceSides != 0) ? ForceSides : (ceil(Dia) + 2);
	FixDia = Dia / cos(180/Sides);
	cylinder(r=(FixDia + HoleWindage)/2,
	h=Height,
	$fn=Sides);
	}

	// Basic shapes

	// Overall phone outline

	module Phone() {

	hull()
	for (i=[-1,1], j=[-1,1], k=[-1,1])
	translate([i(Phone.x/2 – PhoneRadii.x),j(Phone.y/2 – PhoneRadii.y),k*(Phone.z/2 – PhoneRadii.z)])
	resize(2*PhoneRadii)
	sphere(r=1,$fn=NumSides);
	}

	module Plate() {

	union() {
	difference() {
	union() {
	hull()
	for (i=[-1,1], j=[-1,1])
	translate([i(Plate.x/2 – PlateRadius),j(Plate.y/2 – PlateRadius),0])
	cylinder(r=PlateRadius,h=Plate.z,center=true,$fn=NumSides);
	translate([Phone.x/2,Phone.y/2,-Eyepiece[LENGTH]/3 + Plate.z/2] + LensOffset)
	cylinder(d=Eyepiece[OD] + 2*WallThick,h=Eyepiece[LENGTH]/3,
	center=false,$fn=NumSides);
	translate([Phone.x/2,Phone.y/2,-2*Eyepiece[LENGTH]/3 + Plate.z/2 + Protrusion] + LensOffset)
	cylinder(d1=Eyepiece[OD] + 10*ThreadThick,
	d2=Eyepiece[OD] + 2*WallThick,
	h=Eyepiece[LENGTH]/3,
	center=false,$fn=NumSides);
	}
	translate([Phone.x/2,Phone.y/2,-2*Eyepiece[LENGTH] + Plate.z/2 + Protrusion] + LensOffset)
	PolyCyl(Eyepiece[OD],2*Eyepiece[LENGTH],NumSides);
	translate(PrintReader + [0,0,-Plate.z/2 – Protrusion])
	cylinder(d1=PrintReaderDia[OD],d2=PrintReaderDia[ID],h=Plate.z + 2*Protrusion,$fn=NumSides);
	for (i=[-1,1], j=[-1,1])
	translate([i(Phone.x/2 + Bumper.x/2),j(Phone.y/2 – Bumper.y/2),-Plate.z])
	PolyCyl(Insert[OD],2*Plate.z,8);
	for (i=[-1,1], j=[-1,1])
	translate([i(Phone.x/2 – Bumper.y/2),j(Phone.y/2 + Bumper.x/2),-Plate.z])
	PolyCyl(Insert[OD],2*Plate.z,8);

	translate([0,-12,Plate.z/2]) // recess for legend
	cube([55,40,EmbossDepth],center=true);
	}

	translate([0,0,Plate.z/2 – EmbossDepth])
	linear_extrude(height=DebossHeight,convexity=20)
	text(text="Pixel 3a",size=6,spacing=1.20,
	font="Arial:style:Bold",halign="center",valign="center");
	translate([0,-15,Plate.z/2 – EmbossDepth])
	linear_extrude(height=DebossHeight,convexity=20)
	text(text="Ed Nisley",size=6,spacing=1.20,
	font="Arial:style:Bold",halign="center",valign="center");
	translate([0,-25,Plate.z/2 – EmbossDepth])
	linear_extrude(height=DebossHeight,convexity=20)
	text(text="softsolder.com",size=4,spacing=1.20,
	font="Arial:style:Bold",halign="center",valign="center");


	}
	}

	module BumperPiece() {
	difference() {
	translate([0,-BumperOAL/2 + Bumper.x,0])
	hull()
	for (i=[-1,1], j=[-1,1])
	translate([i(Bumper.x/2 – BumperRadius),j(BumperOAL/2 – BumperRadius),0])
	cylinder(r=BumperRadius,h=Bumper.z,center=true,$fn=NumSides);
	translate([0,-Bumper.y/2,-Bumper.z])
	PolyCyl(ScrewAdjust,2*Bumper.z,8);
	}
	}

	// Side bumpers, XY origin at inner corner

	module BumperCorner() {

	union() {
	translate([Bumper.x/2,0,0])
	BumperPiece();
	translate([0,Bumper.x/2,0])
	rotate(-90)
	BumperPiece();
	}
	}


	//- Build things

	if (Layout == "Phone")
	Phone();

	if (Layout == "Plate")
	Plate();

	if (Layout == "Bumper")
	BumperCorner();

	if (Layout == "Show") {
	color("LightBlue") Plate();
	for (i=[-1,1], j=[-1,1]) {
	a =
	i > 0 && j > 0 ? 0 :
	i < 0 && j > 0 ? 90 :
	i > 0 && j < 0 ? -90 :
	180
	;
	translate([iPhone.x/2,jPhone.y/2,Plate.z/2 + Bumper.z/2])
	rotate(a)
	color("LightGreen") BumperCorner();
	translate([0,0,Phone.z/2 + Plate.z/2 + Protrusion])
	color("DarkGray",0.5) Phone();
	}
	}

	if (Layout == "BuildAll") {
	translate([0,0,Plate.z/2])
	rotate([0,180,0])
	Plate();
	for (i=[-1,1], j=[-1,1]) {
	a =
	i > 0 && j > 0 ? 0 :
	i < 0 && j > 0 ? 90 :
	i > 0 && j < 0 ? -90 :
	180
	;
	translate([i(Plate.x/2 + Gap),j(Plate.y/2 + Gap),Bumper.z/2])
	rotate(a)
	BumperCorner();
	}
	}


	if (Layout == "BuildPlate") {
	translate([0,0,Plate.z/2])
	rotate([0,180,0])
	Plate();
	}


	if (Layout == "BuildBumpers") {
	for (i=[-1,1], j=[-1,1]) {
	a =
	i > 0 && j > 0 ? 180 :
	i < 0 && j > 0 ? -90 :
	i > 0 && j < 0 ? 90 :
	0
	;
	translate([i(Bumper.x + Gap),j(Bumper.x + Gap),Bumper.z/2])
	rotate(a)
	BumperCorner();
	}
	}


	if (Layout == "DrillGuide") {
	projection(cut=true)
	Plate();

	}

view raw Google Pixel 3a Zoom Microscope Mount.scad hosted with ❤ by GitHub

2019-12-24

Tour Easy: Fairing Strut Mounts, Redux

Our Young Engineer’s Tour Easy followed us home, due to a non-survivable cycling commute and inadequate apartment storage space. What with its Zzipper fairing being off and having easy access to the strut, I conjured & installed another set of fairing mounting blocks:

Tour Easy - Fairing Strut Mount Blocks — Tour Easy – Fairing Strut Mount Blocks

Should you be in need of a Tour Easy recumbent in good shape, well, have I got a deal for you. I’ll even conjure a Daytime Running Light mount, if that’s what it takes …

2019-12-22

Homage Tektronix Circuit Computer: Ball-point Pens vs. Paper

Extra Fine Pilot V5 pens have a 0.5 mm ball, in contrast to the 1.0 mm ball in the cheap pens I’ve been using, so they should produce much finer lines.

Which turns out to be the case:

Tek Circuit Computer - pen and paper comparison — Tek Circuit Computer – pen and paper comparison

That’s a stack of three “Homage” Tek CC bottom decks under a Genuine Tektronix Circuit Computer.

The black scale at the top of the picture (and the bottom of the stack) came from a 1 mm cheap pen in the collet holder, the two green scales come from a 0.5 mm Pilot V5RT cartridge in its new holder, and the Original is (most likely) laser-printed back when that was a New Thing.

As always, paper makes a big difference in the results. The brownish paper is 110 pound card stock with a relatively coarse surface finish. The white paper is ordinary 22 pound general-purpose laser / inkjet printer paper.

The 1.0 mm pen (top) doesn’t much care what it’s writing on, producing results on the low side of OK: some light sections, no blobs. Perfectly serviceable, but not pretty.

The Pilot V5RT really likes better paper, as it bleeds out on the card stock whenever the CNC 3018XL so much as pauses at the end of a stroke. Using white paper slows, but doesn’t completely stop, the bleeding, making the blobs survivable.

I’ve been using card stock to get stiffer, more durable, and more easily manipulated decks, but the improved line quality on the white paper says I should laminate the decks in plastic, just like the original Tektronix design.

No surprise there!

2019-12-20

Google Pixel 3a Photomicrography vs. Ballpoint Pens

The Google Pixel 3a camera, unlike the camera in my older Google Pixel XL, takes spectacularly good images through a widefield 5X eyepiece on the stereo zoom microscope:

0.5 1.0 mm ball pens - 0.7 mm lead pencil — 0.5 1.0 mm ball pens – 0.7 mm lead pencil

That’s hand-holding the phone against the eyepiece while manipulating it with the other hand. Definitely not the most stable arrangement, but the camera copes well with slight motions. I really need a gripping hand for the camera, to free up another for the microscope’s focus knob.

For the record:

Zooming in (because it’s a stereo zoom microscope and I can), the 1.0 mm ball seems surprisingly un-wetted by its ink:

The Pilot V5 ball seems more smoothly covered:

Those are at the same magnification & crop size, so they’re to the same scale.

This definitely calls for a customized phone-to-eyepiece holder!

2019-12-19