Improvements – Page 132 – The Smell of Molten Projects in the Morning

Tour Easy Daytime Running Light: Fairing Clamp Plates

For reasons obvious to any cyclist, we must improve the forward conspicuity of our Tour Easy recumbents with a white daytime running light; a near-miss boosted this to the front of the project queue. While you can outfit a standard bike with a handlebar-mounted headlight (*), at any price from the sublime to the ridiculous, the smooth snout of a fully faired recumbent covers all the usual attachment points.

A small LED flashlight tacked onto the fairing support bracket seems workable enough to make up for a significant case of ugly:

Tour Easy - J5 Tactical V2 - front — Tour Easy – J5 Tactical V2 – front

That’s a J5 Tactical V2 flashlight on my bike.

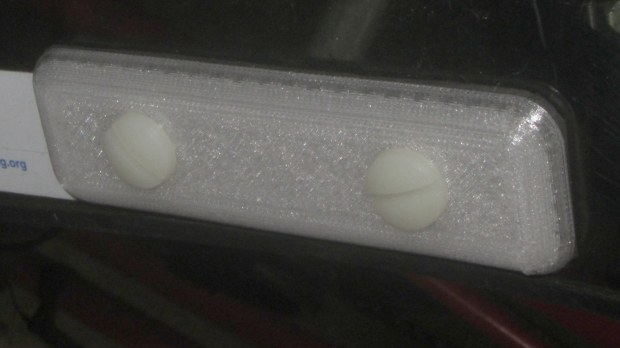
Mary’s bike has a tidier Anker LC40 in an earlier mount version:

Tour Easy - Anker LC40 - front — Tour Easy – Anker LC40 – front

The Anker required an adapter to hold an 18650 cell in its 3xAAA-size body. The J5 V2 is resolutely 18650-only, which is fine with me.

The intent here is to find out whether this works, figure out the proper aiming point(s), then de-bulk the mount.

The next few posts will cover various bits & pieces of the design, because I must remember why I did things the way they turned out: sometimes the obvious choices didn’t work.

The Zzipper fairing originally mounted to the strut across the handlebars with a single 1/4-20 nylon screw on each side. Even with a nylon washer on the outside, the stress concentration cracked the polycarbonate sheet around the screws and brackets, so I designed & printed flat ABS plates to spread the stress over a larger area:

Fairing mount - inside — Fairing mount – inside

The tapered edges were supposed to be flexible, but the foam sheets sandwiched on both sides of the fairing actually provided most of the compliance. There’s another screw in the open hole binding the inner & outer plates together.

The mounts worked perfectly, even as they faded over the years. The fairings became quite scuffed during the course of our near-daily rides, but, heck, we’re also a bit scuffed and it’s still all good.

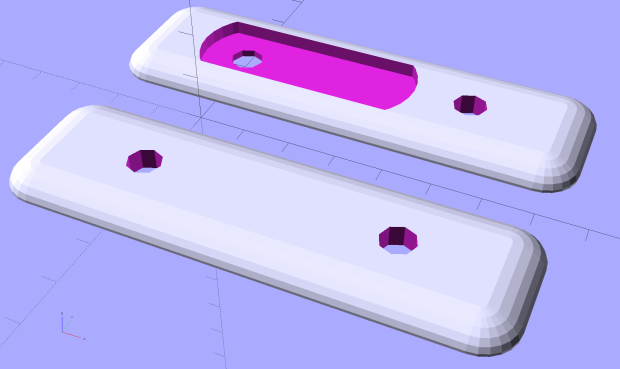
The new PETG inner plates seat on the bracket to nearly its full thickness:

Tour Easy - Zipper fairing plate - inside — Tour Easy – Zipper fairing plate – inside

The flashlight on the outer plate applies torque around the bolt which (I hope) the sides of the recess can resist. This is the absolutely key part of the design and, I’m somewhat ashamed to admit, took me far too long to figure out. What you don’t want: weird & fragile gimcrackery clamped onto the strut extending under the fairing’s edge, with the flashlight hanging far off to the side.

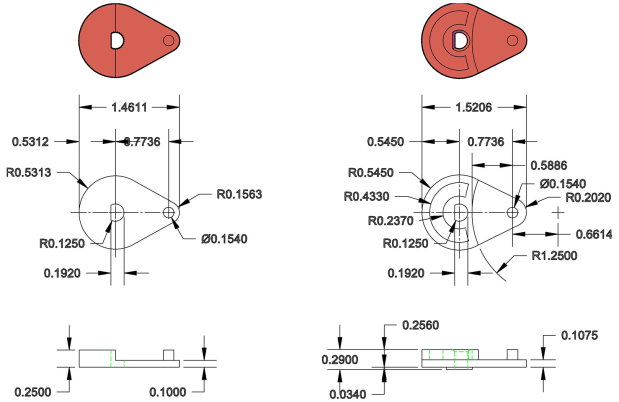
I modeled the fairing strut’s aluminum bracket as a 2D rectangle, plus a pair of chords, embiggened by a thread around the outside edge, minus the hole, then extruded to the proper height:

	//- Fairing Bracket
	// Magic numbers taken from the actual fairing mount
	// Centered on screw hole

	/* [Hidden] */

	inch = 25.4;

	BracketHoleOD = 0.25 * inch; // 1/4-20 bolt holes

	BracketHoleOC = 1.0 * inch; // fairing hole spacing
	// usually 1 inch, but 15/16 on one fairing

	Bracket = [48.0,16.3,3.6 – 0.6]; // fairing bracket end plate overall size
	BracketHoleOffset = (3/8) * inch; // end to hole center

	BracketM = 3.0; // endcap arc height
	BracketR = (pow(BracketM,2) + pow(Bracket[1],2)/4) / (2*BracketM); // … radius

	module Bracket() {

	linear_extrude(height=Bracket[2],convexity=2)
	difference() {
	translate([(Bracket[0]/2 – BracketHoleOffset),0,0])
	offset(delta=ThreadWidth)
	intersection() {
	square([Bracket[0],Bracket[1]],center=true);
	union() {
	for (i=[-1,0,1]) // middle circle fills gap
	translate([i*(Bracket[0]/2 – BracketR),0])
	circle(r=BracketR);
	}
	}
	circle(d=BracketHoleOD/cos(180/8),$fn=8); // dead center at the origin
	}

	}

view raw Fairing Flashlight Mount.scad: Bracket excerpt hosted with ❤ by GitHub

The hole isn’t strictly necessary, as I punch out both screw holes as part of the plate assemblies.

The overall plate shape comes from the top half of a hull() wrapped around four squashed spheres:

	//- General plate shape
	// Centered on the hole for the fairing bracket

	Plate = [100.0,30.0,6*ThreadThick + Bracket[2]];
	PlateRad = Plate[1]/4;

	echo(str("Base plate thick: ",Plate[2]));

	module PlateBlank() {

	difference() {
	translate([BracketHoleOC,0,0])
	intersection() {
	translate([0,0,Plate[2]/2]) // select upper half of spheres
	cube(Plate,center=true);
	hull()
	for (i=[-1,1], j=[-1,1])
	translate([i(Plate[0]/2 – PlateRad),j(Plate[1]/2 – PlateRad),0])
	resize([2PlateRad,2PlateRad,2*Plate[2]])
	sphere(r=PlateRad); // nice rounded corners!
	}
	translate([2*BracketHoleOC,0,-Protrusion]) // screw holes
	PolyCyl(BracketHoleOD,2*Plate[2],8);
	translate([0,0,-Protrusion])
	PolyCyl(BracketHoleOD,2*Plate[2],8);
	}
	}

view raw Fairing Flashlight Mount.scad: Plate Blank excerpt hosted with ❤ by GitHub

Then the inner plate is just a plate blank stamped with the bracket:

	//- Inner plate

	module InnerPlate() {

	difference() {
	PlateBlank();
	translate([0,0,Plate[2] – Bracket[2] + Protrusion]) // punch out fairing bracket
	Bracket();
	}
	}

view raw Fairing Flashlight Mount.scad: Inner Plate excerpt hosted with ❤ by GitHub

You’ll need a set for the side of the fairing without the running light:

Fairing Flashlight Mount - Plates - solid model — Fairing Flashlight Mount – Plates – solid model

The outer plate looks reasonably sleek in real life, although that’s not the primary consideration:

Tour Easy - Zipper fairing plate - outside — Tour Easy – Zipper fairing plate – outside

You could replace the squared-off ends with simple half-circles, maybe stretched into stylin’ ellipse shapes, without too much effort.

I got out the screws, set up to cut them with a pull saw and miter box, then realized they are plastic. Put away the saw, got out the utility knife, and cut them to length with one firm push. No distorted threads, no dust, no muss, no fuss.

(*) Opinion: any headlight with non-replaceable, USB-chargeable cells is a toy. I can replace a discharged (or failed) 18650 cell in the middle of a ride, where a dead battery inside a spendy headlight would leave me in the dark. Might not matter for a DRL, but seems absolutely critical on night rides. ‘Nuff said.

2017-07-19

Layout Pen For Black Objects

This worked surprisingly well to lay out black foam gaskets for new fairing mounting plates:

Black foam layout with ceramic fabric pen

Mary uses the Fons & Porter Mechanical Pencil to mark quilting patterns on fabric. It has, they say, a “strong ceramic 0.9MM white lead” with “water-soluble dyes” capable of both laying down a durable mark and washing out without leaving a trace. I don’t care about the latter, of course, but it did brush off reasonably well.

The next step involved running an X-Acto knife around the perimeter of the plate and punching the holes.

You can get colored ceramic leads (for small values of color) for use on other backgrounds.

2017-07-18

HP 7475A Plotter: Rebuilt Carousel Drive

A followup to the saga of the HP 7475A plotter with a broken carousel drive:

With the information you shared, we were able to successfully model and reconstruct the drive wheel in only a couple of days.

One useful thing we discovered is there’s a lot of room for error – so long as the pin catches and the wheel isn’t slipping on the motor shaft, the mechanism will work. The grooves and the interior radius of the original part aren’t critical.

Because of your heads up about Geneva wheels, I found this excellent website – https://newgottland.com/2012/01/08/make-geneva-wheels-of-any-size/ – which includes a link to a Geneva wheel calculator. With the measurements you sent and a measurement off of the pen carousel, the calculator generated near perfect dimensions for a replacement. There was a little sanding and rounding to fit but it was certainly within tolerance.

Interestingly, the pieces of the drive wheel that I pulled out of the case revealed a small hidden detail. On the underside, there’s a collar around the motor shaft that gives the cam an extra ~.03″ thickness. Presumably this is to help reduce friction during travel. Our prototype doesn’t take this detail into consideration – we’ve had no issues with friction, and we compensated for the thickness by making the pin a little longer – but it’s meaningful to note.

HP7475A Carousel Drive – cam1

The broken pieces also confirmed the thicknesses and radii of the original part, and so my partner was able to build an accurate technical drawing of the drive wheel for future fabrication.

While we intend to make a better replacement, our prototype was built with dense 1/8″ mat board, PVA glue, binder clips, and a short piece of wooden dowel from our bits box. Basically just stuff we had kicking around the studio. It’s held up shockingly well. A little dented around the edges from hitting the carousel, but there’s no slippage. I’m thinking I’ll use it until it falls apart, just to see how long it takes.

HP7475A Carousel Drive – repaired – cam2

Attached, find a technical drawing comparing the original drawing to our prototype (measured in good old fashioned 1980s inches); a photo of the retrieved piece, showing the collar on the reverse side; and a photo of the prototype in place. Feel free to share these – everyone deserves a working plotter!

7475a drive wheel

Once the carousel was working, my roommate – an electrical engineer – hooked me up with a custom serial cable, a Raspberry Pi, and a crash course in Python, so now that I can communicate with the plotter, the possibilities are staggering. I’m thrilled to add this machine to my print studio arsenal!

I love a happy ending …

For anyone with a new-to-you plotter, search the blog for 74754A to find info on replacing failed electrolytic capacitors, adapting Sakura Micron pens, refilling old plotter pens, building a serial cable, hacking Chiplotle to actually use hardware handshaking, and plotting Superformulas. Let me know how you got your plotter working!

2017-07-17

Cylindrical Cell Adapter: 18650 to 3xAAA

Anker LC40 flashlights can use either one lithium 18650 cell or an adapter holding three AAA cells. I now prefer 18650 cells, but they’re nigh onto 4 mm smaller than the flashlight ID and rattle around something awful.

I can fix that:

Three new entries appear in the cell dimension table of my OpenSCAD inter-series battery adapter program:

NAME = 0;
ID = 0;       // for non-cell cylinders
OD = 1;
LENGTH = 2;

Cells = [
  ["AAAA",8.3,42.5],
  ["AAA",10.5,44.5],
  ["AA",14.5,50.5],
  ["C",26.2,50],
  ["D",34.2,61.5],
  ["A23",10.3,28.5],
  ["CR123A",17.0,34.5],
  ["18650",18.8,65.2],
  ["3xAAA",21.2,56.0],
  ["AnkerLC40",23.0,55.0]           // Flashlight tube loose-fit for 3xAAA adapter
];

I took the opportunity of adding OpenSCAD Customizer comments, which means this now works:

OpenSCAD Customizer - dropdown selections — OpenSCAD Customizer – dropdown selections

The model looks about the same as before, although with a few more sides just for pretty:

AnkerLC40 vs. 18650 Sleeve - Slic3r — AnkerLC40 vs. 18650 Sleeve – Slic3r

That was easy …

2017-07-14

AT26 / TF26 Quartz Resonator Identification

There’s not much room on an AT26 / TF26 can for a readable label, unless one owns a metal-marking laser, but a simple bar code should let me identify each one:

Quartz Resonators - binary marking — Quartz Resonators – binary marking

The empty “0” slot down at the bottom will hold the crash-test dummy resonator I’ve been using to get the tester working.

The red-and-blue stripes from plain old fine-point Sharpie pens will rub off under duress, which I hope to avoid. After finishing up, I’m still not sure blue makes a better zero than red; you can make a convincing argument either way:

The bag allegedly contained 25 resonators, although I’m willing to agree the last one escaped into the clutter on or under the Electronics Workbench.

2017-07-11

Crystal Modeling: Parasitic Capacitor Values

A Circuit Cellar reader asked for a better explanation of the parasitic capacitors inside a quartz crystal can than I provided in my April 2017 Circuit Cellar column. Here’s the schematic, with values for a 32 kHz tuning fork resonator and the original caption:

Quartz resonator circuit model — Figure 1 – The mechanical properties of quartz resonators determine the values of the “motional” electrical components in the bottom branch of its circuit model. These values correspond to a 32.768 kHz quartz tuning fork resonator: the 10.4 kH inductor is not a misprint!

I wrote this about the caps:

The value of C0 in the model’s middle branch corresponds to the capacitance between the electrodes plated onto the quartz. The 3.57954 MHz crystal in the title photo, with two silver electrodes deposited on a flat insulating disk, closely resembles an ordinary capacitor. You can measure a crystal’s C0 using a capacitance meter.
However, each of those electrodes also has a capacitance to the resonator’s metal case. The top branch of the model shows two capacitors in series, with Cpar representing half the total parasitic capacitance measured between both leads and the case. Grounding the case, represented by the conductor between the capacitors, by soldering it to the ground plane of an RF circuit eliminates any signal transfer through those capacitors. They will appear as shunt capacitors between the pins and ground; in critical applications, you must add their capacitance to the external load capacitors.

And this about the measurement technique, using a fixture on my AADE LC meter:

With the resonator case captured under the clip on the far right and both its leads held by the clip to the upper left, the meter measures Cpar, the lead-to-case parasitic capacitance. The meter will display twice the value of each parasitic capacitor, at least to a good approximation, because they are in parallel. The five resonators averaged 0.45 pF, with each lead having about 0.25 pF of capacitance to the case. Obviously, measuring half a picofarad requires careful zeroing and a stable fixture: a not-quite-tight banana jack nut caused baffling errors during my first few measurements.
With the resonator repositioned as shown in Photo 2, with one lead under each clip, the meter measures C0, the lead-to-lead capacitance. After careful zeroing, the resonators averaged 0.85 pF.
Although the parasitic lead-to-case capacitors are in parallel with C0, their equivalent capacitance is only Cpar/4 = 0.1 pF. That’s close enough to the measurement error for C0, so I ignored it by rounding C0 upward.

He quite correctly pointed out:

With both leads connected together on one side, then that essentially constitutes a single electrical element inside the case. And with the case being a single element, this configuration in the test fixture seems like a single capacitor with one lead being the case and the other lead being the pins, with a vacuum dielectric.

I would think the meter would display the total capacitance rather than twice the value … It makes sense to me to later say Cpar/2 when the leads are not connected together.

Here’s my second pass at the problem:

… the two-capacitor model comes from the common-case condition, where each lead displays a (nominally equal) parasitic capacitance to the case, because the crystal mounting is reasonably symmetric inside the can. It’s easiest to measure the total capacitance with the leads shorted together, because it’s in the low pF range, then divide by two to get the value of each lead-to-case cap.

[…]

For “real” RF circuits with larger (HC-49 -ish) crystals in parallel-resonance mode, you ground the case and subtract the parasitic capacitance at each lead from the external load capacitors. That’s the usual situation for microprocessor clock oscillators: the crystal sits across the clock amplifier pins, with two more-or-less equal caps from the pins to ground. You should subtract the internal parasitic caps from the clock’s specified load caps, but in practice the values are so small and the cap tolerance so large that it mostly doesn’t matter.

[…]

Un-grounding the case puts those two parasitic caps in series, just as with two discrete caps, so the lead-to-lead capacitance is (or should be!) half of each: 1/4 of the both-leads-to-case value.

Re-reading yet again says I glossed over the effect of having C0 in parallel with the Cpar/2 caps, but methinks dragging those complications into the model benefits only the theoreticians among us (or those working very close to the edge of the possible).

To make it worse, I also botched the QEX reference, which should be Jan/Feb 2016, not 2017. Verily, having a column go read-only makes the errors jump right off the page. [sigh]

At least I can point to this and amend as needed.

2017-07-10

AD9850 DDS Module: 125 MHz Oscillator vs. Temperature, Quadratic Edition

I let the DDS cool down overnight, turned it on, and recorded the frequency offset as a function of temperature as it heated up again:

125 MHz Osc Freq Offset vs Temp - Quadratic - 29 - 43 C — 125 MHz Osc Freq Offset vs Temp – Quadratic – 29 – 43 C

The reduced spacing between the points as the temperature increases shows how fast the oscillator heats up. I zero-beat the 10 MHz output, scribbled the temperature, noted the offset, and iterated as fast as I could. The clump of data over on the right end comes from the previous session with essentially stable temperatures.

I only had to throw out two data points to get such a beautiful fit; the gaps should be obvious.

The fit seems fine from room (well, basement) ambient up to hotter than you’d really like to treat the DDS, so using the quadratic equation should allow on-the-fly temperature compensation. Assuming, of course, the equation matches some version of reality close to the one prevailing in the Basement Laboratory, which remains to be seen.

In truth, it probably doesn’t, because the temperature was changing so rapidly the observations all run a bit behind reality. You’d want a temperature-controlled environment around the PCB to let the oscillator stabilize after each increment, then take the measurements. I am so not going to go there.

The original data:

125 MHz Osc Freq Offset vs Temp - 29 - 43 C - data — 125 MHz Osc Freq Offset vs Temp – 29 – 43 C – data

2017-07-06