Tag: CNC

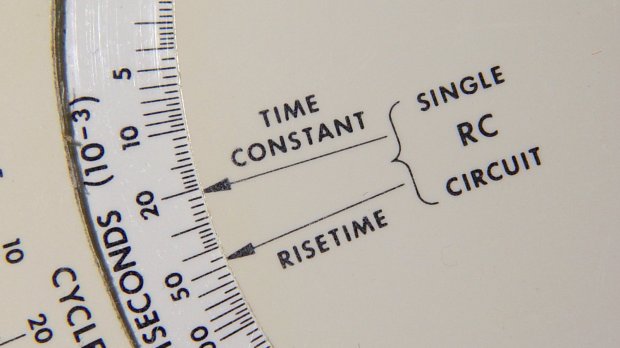
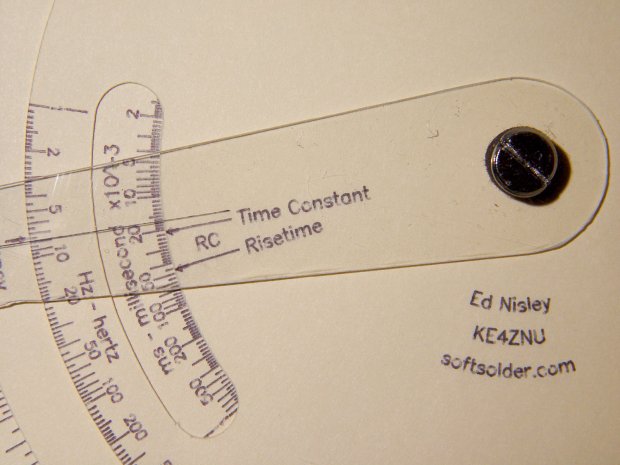
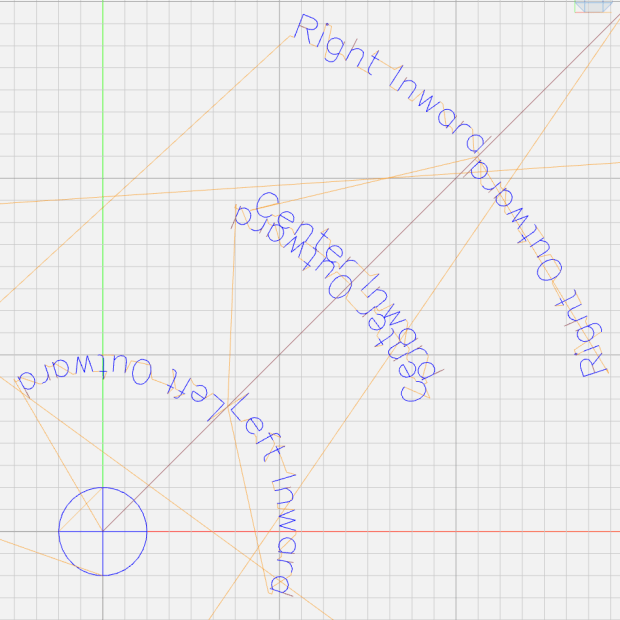
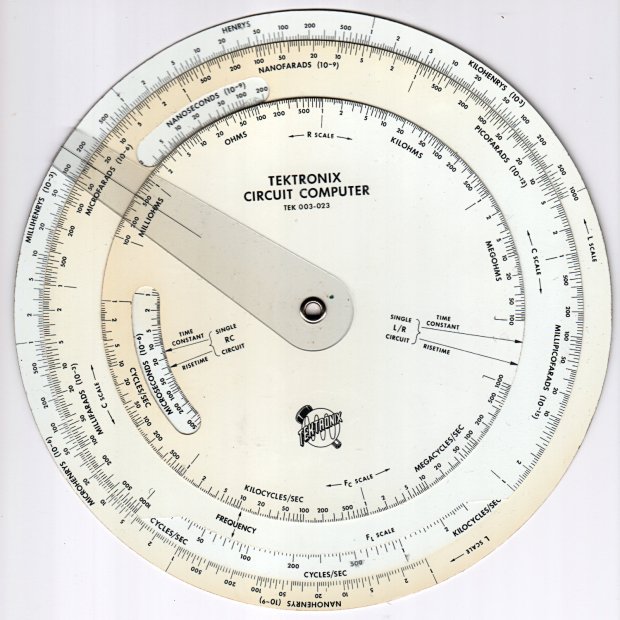
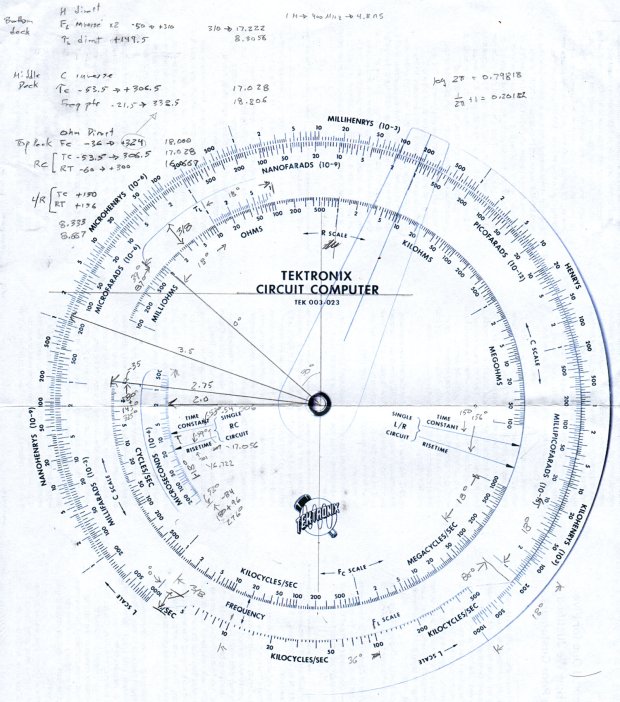
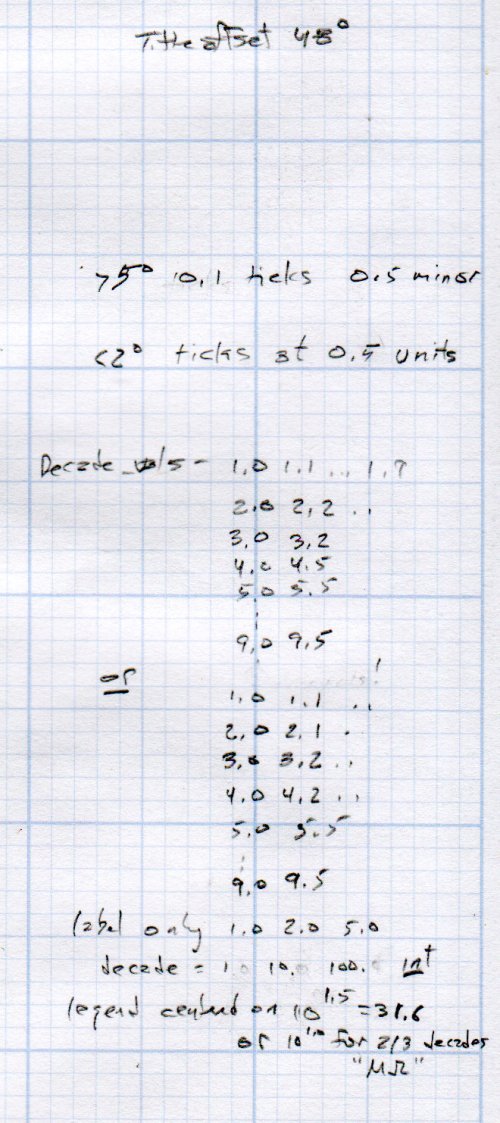The Tektronix Circuit Computer, being a specialized circular slide rule, requires logarithmic scales bent around arcs:

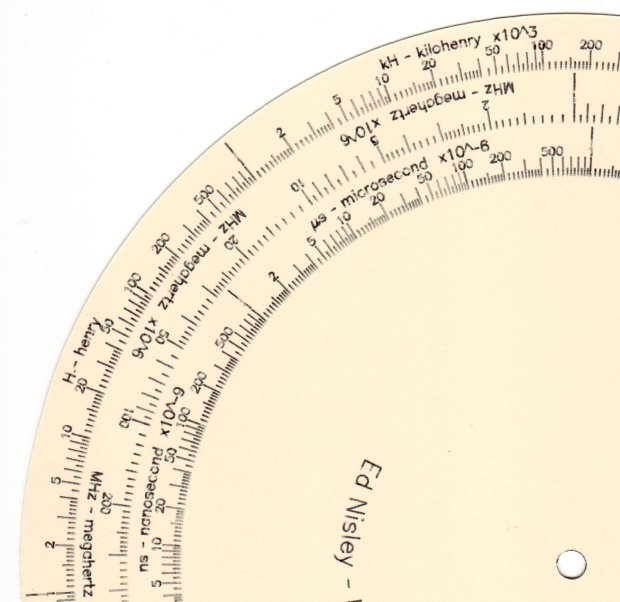
Each decade spans 18°, except for the F_L scale’s 36° span to extract the square root of the LC product:

FL = 1 / (2π · sqrt(LC))

The tick marks can point inward or outward from their baseline radius, with corresponding scale labels reading either inward or outward.

There being no (easy) way to algorithmically set the tick lengths, I used a (pair of) tables (a.k.a. vector lists):

TickScaleNarrow = {
  [1.0,TickMajor],
  [1.1,TickMinor],[1.2,TickMinor],[1.3,TickMinor],[1.4,TickMinor],
  [1.5,TickMid],
  [1.6,TickMinor],[1.7,TickMinor],[1.8,TickMinor],[1.9,TickMinor],
  [2.0,TickMajor],
  [2.2,TickMinor],[2.4,TickMinor],[2.6,TickMinor],[2.8,TickMinor],
  [3.0,TickMajor],
… and so on …

The first number in each vector is the tick value in the decade, the log of which corresponds to its angular position. The second gives its length, with three constants matching up to the actual lengths on the Tek scales.

The Circuit Computer labels only three ticks within each decade in the familiar (to EE bears, anyhow) 1, 2, 5 sequence. Their logs are 0.0, 0.3, and 0.7, spacing them neatly at the 1/3 decade points.

Pop quiz: If you wanted to label two evenly spaced ticks per decade, you’d mark 1 and …

Generating the L (inductance) scale on the bottom deck goes like this:

  Radius = DeckRad - ScaleSpace;

  MinLog = -9;
  MaxLog = 6;
  Arc = -ScaleArc;

  dec = 1;
  offset = 0deg;
  for (logval = MinLog; logval < MaxLog; logval++) {
    a = offset + logval * Arc;
    DrawTicks(Radius,TickScaleNarrow,OUTWARD,a,Arc,dec,INWARD,FALSE);
    dec = (dec == 100) ? 1 : 10 * dec;
  }

  a = offset + MaxLog * Arc;
  DrawTicks(Radius,TickScaleNarrow,OUTWARD,a,Arc,100,INWARD,TRUE);

The L scale covers 1 nH to 1 MH (!), as set by the MinLog and MaxLog values. Arc sets the angular size of each decade from ScaleArc, with the negative sign indicating the values increase in the clockwise direction.

The first decade starts with a tick labeled 1, so dec = 1. The next decade has dec = 10 and the third has dec = 100. Maybe I should have used the log values 0, 1, and 2, but that seemed too intricate.

The angular offset is zero because this is the outermost scale, so 1.0 H will be at 0° (the picture is rotated about half a turns, so you’ll find it off to the left). All other scales on the deck have a nonzero offset to put their unit tick at the proper angle with respect to this one.

The scales have legends for each group of three decades, positioned in the middle of the group:

  logval = MinLog + 1.5;
  a = offset + logval * Arc;
  ArcLegend("nH - nanohenry  x10^-9",r,a,INWARD);

  logval += 3;
  a = offset + logval * Arc;
  ArcLegend("μH - microhenry  x10^-6",r,a,INWARD);

I wish there were a clean way to draw exponents, as the GCMC Hershey font does not include superscripts, but the characters already live at the small end of what’s do-able with a ballpoint pen cartridge. Engraving will surely work better, but stylin’ exponents are definitely in the nature of fine tuning.

With all that in hand, the scales look just like they should:

The GCMC source code as a GitHub Gist:

The Tektronix Circuit Computer needs text along radial lines:

Fortunately, this doesn’t require nearly as much effort as the text-on-arcs code, because GCMC includes functions to rotate paths around the origin:

return rotate_xy(TextPath,Angle) + CenterPt;

The only trick is figuring out how to handle the justification, given the overall path length:

  local pl = TextPath[-1].x;

  local ji = (Justify == TEXT_LEFT)     ? 0mm :
             (Justify == TEXT_CENTERED) ? -pl/2 :
             (Justify == TEXT_RIGHT)    ? -pl :
             0mm;

A testcase showed it worked:

With that in hand, I took the liberty of slightly simplifying the original Tek layout:

If lives depended on it, one could duplicate the Tek layout, but they don’t and I didn’t. Fancy typography isn’t a GCMC thing.

And, yeah, laser printing is way crisper than a pen drawing.

The GCMC source code as a GitHub Gist:

The Tektronix Circuit Computer scale annotations read both inward (from the center) and outward (from the rim):

It’s surprisingly difficult (for me, anyhow) to see the middle FL Scale as reading upside-down, rather than mirror-image backwards.

This turned into a rewrite of the the read-outward annotation code I used for the vacuum tube reflectors. Eventually the justification and orientation options came out right:

The text baseline sits at the specified radius from the center point, regardless of its orientation, so you must offset the text path by half its height in the proper direction before handing it to the ArcText function.

The testcase shows the invocation ritual:

    ctr = [0mm,0mm];

    tp = scale(typeset("Right Inward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,30mm,45deg,TEXT_RIGHT,INWARD);
    engrave(tpa,TravelZ,EngraveZ);
    tp = scale(typeset("Right Outward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,30mm,45deg,TEXT_RIGHT,OUTWARD);
    engrave(tpa,TravelZ,EngraveZ);

    tp = scale(typeset("Center Inward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,20mm,45deg,TEXT_CENTERED,INWARD);
    engrave(tpa,TravelZ,EngraveZ);
    tp = scale(typeset("Center Outward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,20mm,45deg,TEXT_CENTERED,OUTWARD);
    engrave(tpa,TravelZ,EngraveZ);

    tp = scale(typeset("Left Inward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,10mm,45deg,TEXT_LEFT,INWARD);
    engrave(tpa,TravelZ,EngraveZ);
    tp = scale(typeset("Left Outward",TextFont),ScaleTextSize);
    tpa = ArcText(tp,ctr,10mm,45deg,TEXT_LEFT,OUTWARD);
    engrave(tpa,TravelZ,EngraveZ);

    goto([0mm,0mm,-]);
    move([40mm,40mm,-]);

A utility function to draw scale legends stuffs some of that complexity into a bottle:

function ArcLegend(Text,Radius,Angle,Orient) {

  local tp = scale(typeset(Text,TextFont),LegendTextSize);
  local tpa = ArcText(tp,[0mm,0mm],Radius,Angle,TEXT_CENTERED,Orient);

  feedrate(TextSpeed);
  engrave(tpa,TravelZ,EngraveZ);
}

Which means most of the text uses a simpler invocation:

  r = Radius + TickMajor + 2*TickGap + LegendTextSize.y;

  logval = MinLog + 1.5;
  a = offset + logval * Arc;
  ArcLegend("nH - nanohenry  x10^-9",r,a,INWARD);

  logval += 3;
  a = offset + logval * Arc;
  ArcLegend("μH - microhenry  x10^-6",r,a,INWARD);

Arc determines the angular span of each decade, with positive values going counterclockwise. MinLog is the logarithm of the scale endpoint, so adding 1.5 puts the text angle one-and-a-half decades from MinLog and multiplying by Arc moves it in the right direction. The offset angle rotates the entire scale with respect to the 0° reference sticking out the X axis over on the right. The top picture has its 0° reference pointing north-northeast.

The GCMC source code as a GitHub Gist:

GCMC treats variables defined inside a function as local, unless they’re already defined in an enclosing scope, whereupon you overwrite the outer variables. This wasn’t a problem in my earlier programs, but I fired the footgun with nested functions using the same local / temporary variables. Now, I ruthlessly declare truly local variables as local, except when I don’t, for what seem good reasons at the time.